Функції, матриці і ранжовані змінні

В формулах можуть використовуватися стандартні функції. В Mathcad визначено багато стандартних функцій ( математичних, статистичних та інших ). Крім того, користувач має можливість ввести ( визначити ) свою власну функцію, яка надалі ( в межах даного доку­менту ) буде використову­ва­тися нарівні зі стандартними функціями. Визначення функції користувача в найпростішому випадку має вид:

<ім'я> ( <список аргументів> ) := <вираз> ,

причому при запису виразу можна використовувати як стандартні функції Mathcad, так і визначені раніше функції користувача. Наприклад,

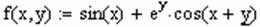
( нагадаємо, що для введення знака присвоювання := досить натиснути клавішу з символом :).

Принципи використання функцій у математичних виразах такі ж, як і в будь-якій мові програмування, тобто після імені функції в дужках обов'язково записуються фактичні параметри ( аргументи ), причому їхній тип, кількість і порядок запису повинні збігатися з передбаченими в описі функції. Вводити функції в вирази можна звичним способом, тобто за допомогою клавіатури. Найбільш вживані математичні функції можуть бути введені також за допомогою панелі елементів Калькулятор (див. рис.10.2).

Крім простих змінних у Mathcad використовуються масиви, тобто сукупності скінченого числа елементів, об’єднані за деякою ознакою під одним спільним іменем. Розрізняють одновимірні масиви ( вектори ) і двовимірні масиви ( матриці ). Доступ до конкретних елементів масиву здійснюється за допомогою цілочисельних індексів. Для елемента вектора вказується один індекс - порядковий номер елемента в сукупності. Для елемента матриці вказуються два індекси: перший - номер рядка, другий - номер стовпчика, на перетині яких знаходиться даний елемент. Розмір матриці характеризується кількістю рядків і стовпчиків. Вектор може розглядатися як окремий випадок матриці, що складається з одного стовпчика або одного рядка.

Для введення матриць у Mathcad необхідно спочатку ввести шаблон, вказавши кількість рядків і стовпчиків, а потім заповнити його конкретними елементами. Введення шаблону здійснюється одним із таких способів:

· через меню (пункти Добавить, Матрицу);

· за допомогою математичної палітри Матрицы (кнопка );

· за допомогою комбінації клавіш Ctrl+M.

Приклади порожніх і частково заповнених шаблонів показані на рис. 10.3.

Рисунок 10.3 - Приклади шаблонів векторів і матриць

Відзначимо, що після визначення вектора або матриці в цілому доступними є також їхні окремі елементи ( наприклад, А₅, М_2,3 ). Перехід до запису індексів здійснюється клавішею [, а до нормального рівня рядка – клавішею пробілу. Для запису операторів виведення або присвоювання переходити до нормального рівня рядка не обов'язково.

Ще один спосіб задання векторів і матриць заснований на використанні ранжованих змінних. Він застосовується у випадках, коли між елементами масиву й індексами елементів можна встановити явну аналітичну залежність.

Ранжована змінна - це спеціальний тип даних із множинними значеннями. Фактично це сукупність значень, що змінюються в заданому інтервалі з деяким кроком.

Для задання ранжованої змінної слід ввести її ім'я, оператор присвоювання, а потім - перше, друге й останнє значення. Наприклад, так:

У цьому прикладі введена змінна х із значеннями 1; 1.5; 2; 2.5; 3 , змінна у із значеннями -2; -1. 3; -0. 6; 0.1; 0.8 і змінна n із значеннями 1, 2, 3, 4, 5. Як бачимо, Mathcad самостійно визначає крок зміни і формує всі члени послідовності, що задається зазначеним вище способом. Відзначимо, що оператор присвоювання, як завжди в Mathcad вводиться клавішею :(двокрапка), а символ продовження послідовності .. вводиться клавішею ;(крапка з комою) . Крок зміни значень може бути не тільки додатним, але і від’ємним. У окремому випадку, коли крок зміни дорівнює 1 або -1, запис спрощується (у наведеному прикладі для змінної n друге значення не зазначене).

Для виведення значень ранжованої змінної використовується звичайний оператор виведення =.

Може здатися, що ранжована змінна - це вектор. Проте, це не так. Головна відмінність полягає в тому, що доступ до одного конкретного значення ранжованої змінної неможливий . У той же час, через ранжовану змінну можна визначати вектори і матриці.

Нехай, наприклад, елементи вектора А обчис­люються за формулою А_i = i² ( i=1,2,... 5 ). Тоді задання вектора виглядає так, як показано на рисунку 10.4. Там же відображений результат виведення на екран вектора А. Як видно, у першому випадку вектор має 6 елементів, незважаючи на те, що ранжована змінна i має 5 значень. Це викликане тим, що нумерація індексів може починатися або з 0, або з 1 у залежності від значення системної змінної ORIGIN. За замовченням ORIGIN=0, тому в першому випадку на друк виведений і нульовий елемент масиву. В другому випадку змінна ORIGIN задана явно ( її значення дорівнює 1, індекси починаються з 1 і вектор містить 5 елементів ).

Відзначимо, що при звертанні до елементів масивів завжди варто мати на увазі значення системної змінної ORIGIN. Особливо це важливо у випадках завдання векторів і матриць за допомогою шаблонів ( див. приклади на рисунку 10.5 ).

І ще одне зауваження, що стосується виведення ранжованих змінних і векторів. Якщо кількість значень змінної або вектора більше 16, то в таблиці виведення відобразяться тільки перші 16 значень. Проте, при виділенні такої таблиці в ній з'являться смуги прокрутки для доступу до інших елементів. Те ж саме має місце і при роботі з матрицями (на екрані спочатку буде видно 16 рядків і 10 стовпчиків).

10.5 Побудова та опрацювання двовимірних графіків

Для побудови графіків у середовищі Mathcad використовуються шаблони, доступ до яких забезпечується спеціальною палітрою График або ж через систему меню ( пункти Добавить, Графики ). Користувач може вибрати один із 7 типів графіків: два з них є двовимірними ( X-Y график і Полярный график ), інші відносяться до тривимірних або так називаних 3D-графіків.

Технологія створення графіків досить проста: готується інформація для графіка; викликається шаблон потрібного типу й у місця введення (вони відзначені чорними прямокутниками) вводяться необхідні параметри. Після цього достатньо просто клацнути мишею поза межами графіка: графік відразу ж відобразиться на екрані.

Відзначимо, що ступінь участі користувача в побудові графіка може бути різною: цілий ряд параметрів Mathcad може задати самостійно (за замовченням).

Нехай, наприклад, необхідно побудувати графік функції y = x² sin x². Для цього необхідно:

· ввести з клавіатури вираз x² sin x² ;

· вивести на екран палітру График і клацнути мишкою на кнопці X-Y график;

· в шаблоні, що з’явиться, ввести ім'я незалежного аргументу х (на місці чорного квадратику під віссю абсцис);

· клацнути мишею поза межами графіка.

В результаті з'явиться графік, показаний на рисунку 10.6 ліворуч. Треба сказати, що в загальному випадку вигляд графіка обраного типу визначається 6 параметрами: незалежний аргумент, функція, найменше і найбільше значення аргументу, найменше і найбільше значення функції. Ми фактично ввели тільки перші два параметри (без них побудова графіка взагалі неможливо), інші Mathcad прийняв за замовченням (для аргументу завжди приймається інтервал [-10, 10]; інтервал для функції вибирається таким, щоб усі її значення потрапили на графік).

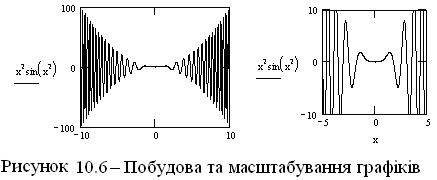
Якщо вигляд графіка не влаштовує користувача, то можна внести деякі зміни. Зокрема, можна змінити будь-який із зазначених вище параметрів графіка. Для цього варто виділити графік клацанням миші на ньому, установити курсор миші біля потрібного параметра і відредагувати його значення, забираючи непотрібні символи і вводячи потрібні. Саме так отриманий графік, показаний на рисунку 10.6 праворуч (в ньому змінені найменші і найбільші значення аргументу і функції) .

Побудований графік при необхідності можна збільшити або зменшити, а також перенести в інше місце. Для виконання будь-якої з цих дій необхідно, насамперед, виділити графік клацанням миші на ньому. Навколо графіка з'явиться прямокутна рамка з квадратиками на правій і нижній межах, а також у правому нижньому куту. "Схопивши" мишкою за один із цих квадратиків, можна графік збільшити або зменшити. Для переміщення графіка слід спочатку встановити курсор миші поблизу межі так, щоб він прийняв вигляд долоні руки; потім натиснути ліву кнопку миші і, не відпускаючи її, перемістити графік у потрібне місце.

Для внесення інших змін слід перейти у вікно форматування, що викликається або через головне меню (пункти Формат і Графики); або через контекстне меню, викликане клацанням правої кнопки мишки на графіку (пункт Формат…). У цьому вікні можна уточнити вигляд і стиль осей графіка; задати вид і колір кривої на графіку; підписати графік і будь-яку з осей і т.п.

Функцію не обов'язково записувати на самому графіку. Її можна визначи­ти раніше як функцію користувача і тоді на графіку досить просто зазначити ім'я функції (див. приклад на рисунку 10.7 ліворуч ).

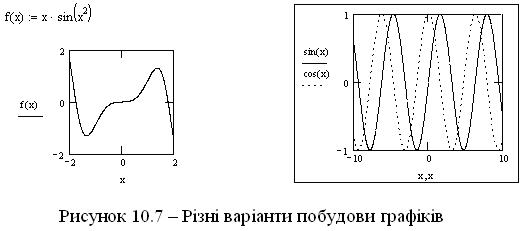
Можна побудувати і кілька кривих на одному графіку. Для цього достатньо просто перерахувати через кому відповідні математичні вирази або імена функцій у шаблоні введення по осі ординат. При відображенні вони будуть записані одна над одною, причому під кожною буде показано, як саме ця крива відображається (див. приклад на рисунку 10.7 праворуч).

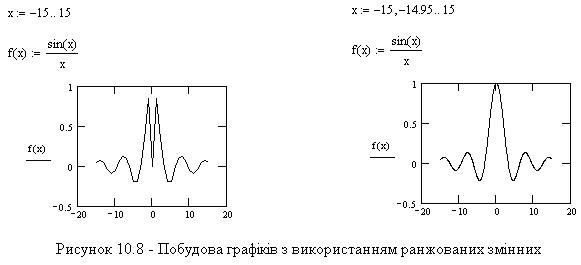
Ще одне зауваження стосується точності побудови графіка. При по­бу­­довах враховується скінчене число точок, обумовлене Mathcad авто­матично. Іноді це призводить до втрати істотних особливостей графіка. Втрутитися в процес завдання опорних точок користувач може шляхом застосування ранжованих змінних (див. приклади на рисунку 10.8). У цьому випадку для всіх значень ранжованої змінної обчислюються значення заданої функції і координати всіх отриманих точок використовуються при побудові графіка. Само собою зрозуміло, що крок зміни ранжованої змінної (фактично: кількість точок) впливає на точність побудови. Саме це продемонстровано на поданих графіках.

Графік функції можна переглядати цілком або окремими ділянками (у збільшеному вигляді). Для зміни масштабу відображення деякої області графіка в декартовій системі координат слід насамперед виділити графік і викли­кати вікно зміни масштабу (команда Масштаб контекстного меню або пункти головного меню Формат, Графики, Масштаб). Далі варто виділити потрібну область, намалювавши мишкою пунктирну рамку (у вікні зміни масштабу Масштаб X-Y з'являться координати точок, що визначають діаго­наль рамки) і клацнути мишкою по кнопці для збільшення масшта­бу. Перехід до первинного відображення графіка здійснюється кнопками або .

Ще одна можливість дослідження графіка надається трасуванням. Вікно трасування визивається командою Трассировка контекстного меню або ж послідовністю команд головного меню Формат, Графики, Трассировка. Після появи вікна Трассировка X-Y достатньо клацнути мишкою в будь-якій точці графіка, щоб у вікні трасування з'явилися координати цієї точки, а на самому графіку - перехрестя двох перпендикулярних ліній, що перетинаються в даній точці (див. рисунок 10.9). Надалі можна плавно переміщати перехрестя мишкою або ж просто клацнути в іншому місці.

Координати будь-якої точки можна помістити в буфер обміну (кнопки Copy X або Copy Y вікна X-Y Trace), а потім вставити в документ.

Відзначимо , що у вікні трасування є перемикач След точек данных. Якщо він включений, то перехрестя автоматично зміщується до найближ­чої точки на кривій (так забезпечується зняття точних координат кривої).

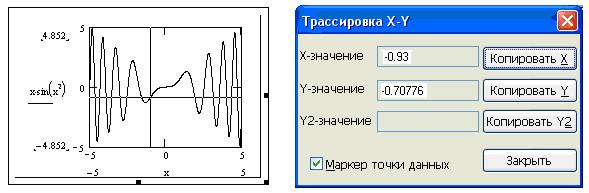
Рисунок 10.9 – Приклад трасування графіка

10.6 Побудова та форматування тривимірних графіків

При побудові тривимірних графіків поверхонь спочатку вводиться відповідний шаблон за допомогою палітри График або головного меню (Добавить, Графики, График поверхности). У цьому шаблоні тільки одне місце введення: у лівому нижньому куту. Саме сюди вводиться інформація про аплікати (координати Z) поверхні. Після введення цієї інформації достатньо клацнути мишкою поза областю графіка для його появи на екрані.

Залежність аплікати від інших координат може бути задана звичайною функцією, наприклад, Z=cos xy (див. рисунок 10.10, ліворуч ).

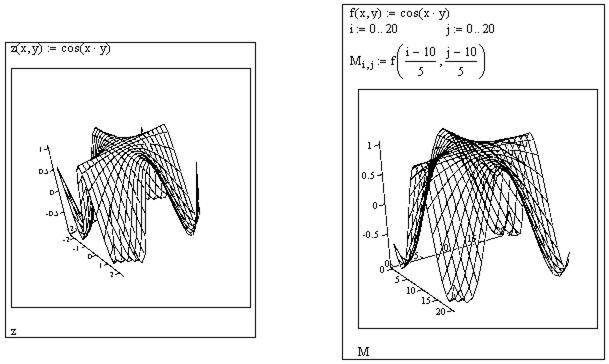
Рисунок 10.10 – Приклади побудови графіків поверхонь

Іншим способом є задання матриці аплікат (див. рис.1.14, праворуч). При цьому координати х і у повинні бути певним чином пов'язані з індексами матриці.

Для більш ефектного представлення побудовані графіки поверхонь звичайно форматують. Багаті можливості для цього даються діалоговим вікном форматування, доступ до якого здійснюється через головне меню (пункти Формат і Графики) або через контекстне меню, викликане клацанням правої кнопки мишки на графіку (пункт Свойства).

У деяких випадках вигляд графіка можна істотно поліпшити шляхом повороту системи координат на деякий кут. У Mathcad реалізована дуже зручна процедура обертання графіка за допомогою миші: достатньо просто "схопити" мишкою за деяку точку області графіка, після чого графік повер­тається в ту або іншу сторону в залежності від переміщення мишки. Саме в такий спосіб отримані графіки на малюнку вище.

Якщо переміщати мишку при натиснутій лівій кнопці і при цьому ще утримувати натиснутою клавішу Ctrl, то можна наближати або віддаляти графік, що також змінює його зовнішній вигляд.

Якщо ж трохи пообертати графік при натиснутій клавіші Shift, а потім відпустити кнопку миші ( і клавішу Shift), то графік буде сам обертатися в заданому напрямку, надаючи можливість огляду поверхні з різних точок. Для припинення обертання достатньо буде клацнути мишкою на графіку.

10.7 Символьні обчислення в середовищі Mathcad

У середовищі Mathcad символьні обчислення можуть виконуватися або за допомогою системи меню ( пункт Символика ), або за допомогою оператора символьних перетворень ®. У першому випадку дії виконуються над явно заданою функцією, у другому - можна використовувати і визначені раніше функції користувача. При використанні оператора символьних перетворень ®деякі операції можуть бути задані відповідними директивами палітри Символы, а деякі - за допомогою шаблонів палітри Исчисление.

При виконанні символьних обчислень за допомогою палітри Исчисление застосовується така процедура:

· на екран виводять палітри Исчисление і Вычисление (див. рис. 10.11);

· клацанням миші на відповідному шаблоні палітри Исчисление вводиться шаблон потрібної операції (див. таблицю 10.2);

· заповнюються місця введення шаблона відповідною інформацією;

· вводиться оператор символьних перетворень ® клацанням миші на цьому знаку в палітрі Вычисления (або за допомогою комбінації клавіш Ctrl+.);

· після клацанням миші поза областю введення на екрані з'являється результат.

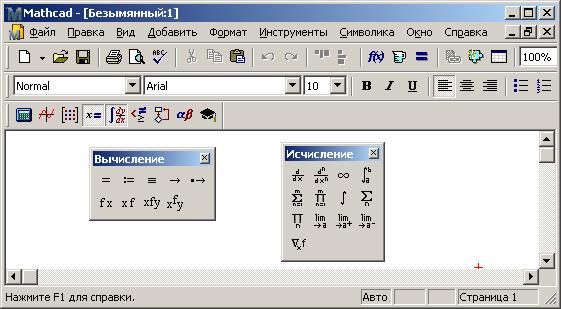
Рисунок 10.11 – Палітри Исчисление і Вычисление

Зауважимо, що в прикладі на суму скінченого ряду (див. табл. 10.2) результат символьної операції у вигляді звичайного дробу виявився не дуже наочним, тому остаточний результат у вигляді десяткового дробу отриманий після введення символу = , тобто після активізації режиму обчислень.

Таблиця 10.2 - Основні символьні операції Mathcad

Назва операції	Шаблон	Приклад
Границя функції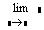
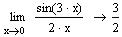
Похідна функції однієї змінної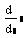
Похідна вищого порядку від функції однієї змінної
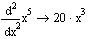
Часткова похідна функції багатьох змінних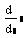
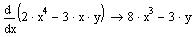
Часткова похідна вищого порядку
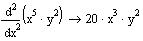
Змішана похідна функції багатьох змінних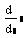
Невизначений інтеграл (первісна)
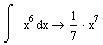
Визначений інтеграл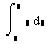
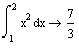
Невласний інтеграл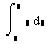
Кратні інтеграли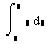
Сума скінченого ряду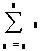
Сума збіжного числового ряду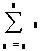

10.8 Символьне розв’язування нелінійних рівнянь

Для одержання розв’язку нелінійного рівняння f(x)=0 у символьному вигляді (тобто, аналітичного розв’язку) можна використовувати один із таких способів:

1) записати вираз f(x), виділити змінну х і відпрацювати пункти меню Символика, Переменная, Решить;

2) за допомогою математичної палітри Символьная ввести шаблон 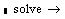, на місці чорного прямокутника записати вираз f(x), потім клацнути мишею поза межами шаблона.

Як наслідок будь-якої з цих дій з'явиться вектор коренів рівняння (див. приклади на рисунку 10.12). Зауважимо, що в останньому прикладі після одержання символьного розв’язку був застосований ще оператор виведення, що дозволило перейти до наближеного розв’язку у вигляді десяткового дробу.

З наведених прикладів ясно, що розв’язок рівнянь у символьному вигляді має сенс насамперед тоді, коли в рівняннях є параметри (можна одержати розв’язок в узагальненому вигляді, а потім вже обчислювати значення коренів при конкретних значеннях параметрів).

Окрім того, розв’язуючи рівняння у символьному вигляді, користу­вач має можливість знайти точні розв’язки конкретних рівнянь, вира­жені через радикали, комплексні числа або ірраціональні числа типу p.