Розв'язання нелінійних рівнянь і систем рівнянь за допомогою обчислювального блоку Given

Універсальним засобом розв'язання нелінійних рівнянь і систем рівнянь є використання спеціального обчислювального блока, загальна структура якого така:

Початкові умови

Given

Рівняння

Обмежувальні умови

Вирази з функціями Find або Minerr.

Як бачимо, у цьому випадку спочатку за допомогою звичайного оператора присвоювання задаються початкові значення шуканих змінних. Потім після службового слова Given записуються рівняння ( ліва і права частина відокремлюються так званим жирним знаком рівності, який вводиться натисканнямCtrl+= ) та обмежувальні умови у вигляді рівностей або нерівностей. Останньою записується одна з зазначених вище функцій із відповідними параметрами.

При цьому функції Find і Minerr мають однакове призначення й однакову структуру

Find(х₁ , х₂ ,... , х_n); Minerr (х₁ , х₂ ,... , х_n) .

Проте, є істотна відмінність. Функція Find дозволяє знайти наближене розв'язання тільки тоді, коли початкові наближення задані вдало, а розв'язання взагалі існує. Функція Minerr у будь-якому випадку знаходить такі значення шуканих змінних, які краще інших наближають рівняння й обмежувальні умови. Хоч знайдені значення можуть і не бути розв'язанням в загальноприйнятому розумінні, але в деяких практичних випадках такий підхід має сенс.

На рисунку 10.15 показаний приклад знаходження додатнього кореня рівняння 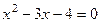. На перших двох кадрах видно, що при завданні початкового наближення х=3 обидві функції дають вірну відповідь. Якщо ж у якості початкового наближення задати х=1, то при використанні функції Find Mathcadпросто не дає ніякого результату (при цьому наближенні метод не сходиться до додатнього кореня рівняння). При використанні функції Мinеrr Mathcadдає результат, але отримана відповідь не є правильною. Просто зна­чен­ня х₁= -0,6 виявилося тим, яке ближче усього до накладених умов ( рівняння й обмежень ).

Рисунок 10.15 - Приклади використання обчислювального блоку Given

Два останніх кадри рисунку 10.15 показують, що якщо обмеження х>0 зняти, то обидві функції у випадку початкового наближення х=1 сходяться до другого кореня аналізованого рівняння.

На рисунку 10.16 показаний також приклад розв'язання системи нелінійних рівнянь

.

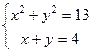Як видно, результат поданий у вигляді вектора-стовпчика з двох елементів. Зауважимо, що при використанні функції Find результат буде таким же.

До речі, із використанням обчислювального блока Given можна одержувати і символьні розв'язання ( див. приклад нижче).

Рисунок 10.17 - Приклад символьного розв'язку

Контрольні запитання до теми 10

1. В чому полягає особливість комп’ютерної математики порівняно зі звичайною математикою?

2. Перерахуйте основні математичні пакети прикладних програм. Чим вони відрізняються від інших програм обчислювального характеру (наприклад, Excel)?

3. Опишіть основні принципи роботи з пакетом MathCad .

4. Для чого в MathCad використовується палітра математичних знаків Калькулятор?

5. Опишіть правила введення арифметичних виразів та процедуру обчислення їх значень.

6. Як в MathCad описуються власні функції користувача? Як вони надалі використовуються?

7. Як в MathCad вводяться і виводяться вектори і матриці?

8. Що таке ранжовані змінні? Чим ранжована змінна подібна до вектора, а чим – відрізняється?

9. Яке значення має системна змінна ORIGIN з точки зору використання векторів і матриць?

10. Опишіть процедуру побудови двовимірних графіків.

11. Які можливості по редагуванню графіків надає MathCad ?

12. Для чого при побудові графіків використовуються ранжовані змінні?

13. Опишіть процедуру перегляду графіка в збільшеному масштабі.

14. Опишіть процедуру трасування графіків. Для чого вона використовується?

15. Опишіть процедуру побудови графіків поверхонь в MathCad.

16. Яким чином можна надати графіку поверхні найбільш ефектного вигляду?

17. Що таке символьні обчислення? Як вони виконуються за допомогою палітри Исчисление?

18. Перерахуйте основні символьні операції, які виконуються в MathCad ? Наведіть конкретні приклади.

19. Опишіть процедуру розв’язування нелінійних рівнянь в символьному виді.

20. Опишіть процедуру числового розв’язування систем лінійних алгебраїчних рівнянь за допомогою перетворення матриць. Що змінюється в процедурі при необхідності одержати розв’язок в символьному виді?

21. Опишіть процедуру розв’язування систем алгебраїчних рівнянь за допомогою функції lsolve.

22. Запишіть загальний вигляд функції root та поясніть смисл всіх параметрів.

23. Яке значення для числового розв’язування нелінійних рівнянь має системна змінна TOL ? Як можна змінити величину TOL ?

24. Для розв’язування яких задач використовується функція polyroots? В чому полягає специфіка цієї функції?

25. Опишіть загальну структуру обчислювального блоку Given. Що таке “жирний знак рівності”, коли і як він вводиться?

26. Поясніть відмінність функції Minerr від функції Find. В яких випадках доцільніше використовувати кожну з цих функцій?