Чисельне розв’язування рівнянь

Як відомо, багато рівнянь і системи рівнянь не мають аналітичних (тобто представлених в символьному вигляді) розв’язків. У першу чергу це стосується більшості трансцендентних рівнянь. Однак такі рівняння можуть вирішуватися чисельними методами з заданою точністю.

Для найпростіших рівнянь виду f(x) = 0 числове рішення в Mathcad знаходиться за допомогою функції root . Загальний вид цієї функції:

root( f(х), х, a, b )

Функція повертає значення х, що належить відрізку [a, b], при якому вираз або функція f(х)набуває значення 0. Змінній х перед використанням функції root необхідно присвоїти числове значення. Mathcad використовує його як початкове наближення при пошуку кореня. Параметри a, b-необов'язкові, але якщо використовуються, то повинні бути дійсними числами, причому a < b. При заданих значеннях a, bкорені рівняння за межами відрізку не визначаються.

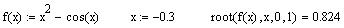
Рисунок 10.13 - Приклади використання функції root

Наближені значення коренів можуть бути відомі з фізичного смислу задачі або ж знайдені попередньо, наприклад, графічним способом.

Якщо після багатьох ітерацій Mathcad не знаходить підхожого наближення, то з'явиться повідомлення (відсутня збіж­ність). Це означає, що початкове наближення обране невірно або ж рівняння взагалі не має коренів.

Для запобігання таких помилок бажано попередньо дослідити графік f(x). Це допоможе з'ясувати наявність коренів рівняння f(x) = 0 і, якщо вони є, то визначити приблизно їх значення. Чим точніше обрано початкове наближення кореня, тим швидше сходиться ітераційний процес визначення кореня з заданою точністю.

Числове значення кореня рівняння є наближеним, його похибка не перевищує заданого значення системної змінної TOL.Для зміни точності, з яким функція root шукає корінь, потрібно змінити значення системної змінної TOL. Для цього слід відпрацювати команді меню Инструменты і Параметры рабочего листа, а потім на вкладці Встроенные переменные встановити в вікні Допустимая сходимость (TOL) потрібне значення. Описане визначення TOL є глобальним, тобто діє для всього документа. Якщо ж потрібно змінити точність в конкретному місці документа, то використовується звичайне присвоєння типу TOL:=0.0001. При збільшенні TOL функція root швидше відшукає наближене значення одного з коренів, але відповідь буде менш точною. Якщо ж значення TOL зменшити, то функція root буде сходитися повільніше, але відповідь буде більш точною.

Зауважимо, що для знаходження коренів полінома виду

a_nxⁿ + ... + a₂x² + a₁x + a₀,

краще використовувати функцію polyroots, ніж root. На відміну від функції root, функція polyroots не вимагає початкового наближення і повертає відразу всі корені, як дійсні, так і комплексні. Загальний вид функції:

polyroots(А)

Функція повертає вектор довжини n, що складає з коренів полінома. Коефіцієнти полінома знаходяться у векторі А довжини n+1. Цей вектор зручно створювати, використовуючи пункти меню Символика і Полиномиальные коэффициенты.

10.10 Розв’язування систем лінійних рівнянь

Розглянемо систему лінійних алгебраїчних рівнянь виду

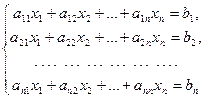
Після введення матриці коефіцієнтів А і векторів-стовпчиків Х (шукані корені рівняння) і В (праві частини рівнянь)

; ;

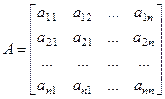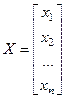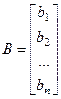
систему можна представити матричним рівнянням

.

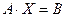Тоді розв’язок має вид

,

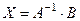де 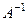- обернена матриця матриці коефіцієнтів системи рівнянь.

До підсистеми символьних обчислень Mathcad входять засоби роботи з матрицями. Завдяки їхній наявності процедура розв’язку вихідної системи рівнянь зводиться до наступного ( див. приклад на рисунку 10.14, ліворуч ):

1) формуються ( вводяться ) матриця коефіцієнтів системи рівнянь А та вектор-стовпчик вільних членів В;

2) записується оператор присвоювання вигляду 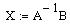( символ 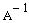вводиться за допомогою математичної панелі Матрица ) ;

3) записується оператор символьного ( або числового ) виведення знайденого вектора Х.

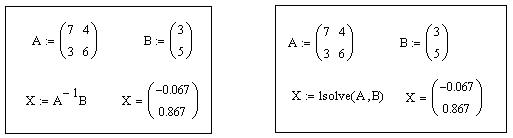
Рисунок 10.14 – Приклади розв'язку системи лінійних рівнянь

Ще один варіант розв’язку системи лінійних алгебраїчних рівнянь у матричному вигляді полягає у використанні функції lsolve (див. приклад на рисунку 10.14, праворуч). Зауважимо, що ця функція вводиться за допомогою клавіатури.