Окремі види рівнянь теплопровідності

Рівняння Пуассона і Лапласа для стаціонарних процесівтеплопровідності. При 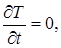рівняння (22) має вигляд

div (l grad T) + q_V = 0 (24)

або при l = const

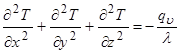(25)

Вираз (25) називають рівнянням Пуассона. При q_v = 0 рівняння Пуассона переходить у рівняння Лапласа.

Рівняння теплопровідності для середовища, що рухається. При русі середовища (тіла) зі швидкістю 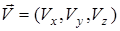основний закон теплопровідності Фур'є має такий вигляд

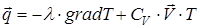(26)

Зокрема, для одновимірного випадку одержуємо

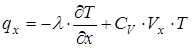(27)

З урахуванням (27) рівняння теплопровідності для середовища, що рухається, уздовж осі Ох (аналогічно, уздовж осей Оу і Oz приймає вигляд

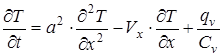(28)

Для приведення рівняння (29) до наступного стандартного (фундаментального) вигляду

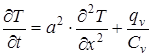(29)

для якого у даний час розроблені класичні методи рішення, використовується підстановка

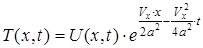(30)

Підставляючи (30) у (28), одержуємо для функції U(x,t) рівняння типу (29)

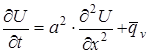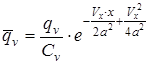, де (30)

Рівняння теплопровідності з рухливим джерелом теплового впливу гаусового типу. Розглянемо випадок теплового впливу на тонкоплівний одновимірний елемент від рухомого джерела тепла, що має гаусовий (чи нормальний) розподіл об'ємної щільності теплового потоку q_v, тобто

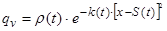, (31)

де r(t) - об’ємна густина теплового потоку в центрі джерела, Вт/м³; 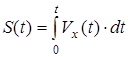- шлях, пройдений центром джерела (при V_x= cons, S = V_x×t), м; k - коефіцієнт зосередженості джерела теплового впливу (гострота теплового імпульсу), м^-2. Підставляючи (31) у (32) одержуємо наступне рівняння теплопровідності з рухливим тепловим впливом

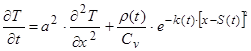(32)

При постійних r, k і V_x рівняння (23) переходить у більш просте рівняння

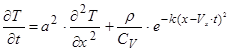, (33)

яке найбільш широко використовується в практичних розрахунках.

Рівняння теплопроводності для високоінтенсивних процесів. Всі попередні рівняння теплопровідності отримані в припущенні нескінченної швидкості поширення тепла в середовищах (або прямуючих до нуля часів релаксації процесів теплопереносу). Однак при надвеликих швидкостях високоінтенсивного джерела теплового впливу необхідно враховувати, що тепло поширюється з кінцевою швидкістю, а основний закон теплопровідності Фур'є має видгляд

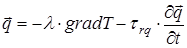, (34)

де t_rq – час релаксації поширення тепла, який звичайно дуже малий (наприклад, для металів t_rq » 10^-11с). При цьому час t_rq визначає швидкість поширення тепла за формулою

W_q = , (35)

яка для металів має порядок W_q »10³ м/c

Таким чином, при обробці матеріалів рухомим джерелом тепла зі швидкістю порядку W_q рівняння теплопровідності для одновимірного випадку буде мати наступний змінений вигляд

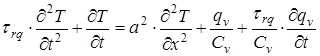(36)

Рівняння (36) можна записати, використавши замість величини t_rq швидкість переносу тепла W_q

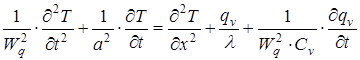(37)

При Wq → ∞ рівняння (37) набуває стандартного вигляду рівняння теплопровідності (29). У приведеному рівнянні (37) додаток 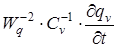вказує, на те що на тепловий баланс впливає не тільки об'ємна густина теплового потоку q_v, але і повна зміна q_v у часі.

Додаток 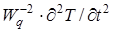показує, що при кінцевій швидкості поширення тепла необхідно враховувати гіперболічний (хвильовий) характер переносу тепла. При цьому кінцеву швидкість поширення тепла в теорії теплопровідності характеризують безрозмірною величиною - числом Верно:

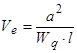, (38)

де l - характерний розмір об‘єкта.

Проведені розрахунки показали, що при V_e > 5...6 необхідно враховувати кінцеву швидкість поширення тепла і використовувати видозмінене рівняння теплопровідності типу (36) чи (37).