Основні поняття і визначення теорії теплопровідності

Температурне поле. Будь-яке фізичне явище відбувається в просторі і в часі, тому вивчення його зводиться до знаходження просторово-часових характеристик величин, що визначають цей процес. Сукупність миттєвих значень фізичної величини у всіх точках розглянутої області називають полем цієї фізичної величини.

У процесах теплопровідності основною фізичною величиною, характерною для даних процесів, є температура. Завдання теплопровідності полягає в знаходженні поля температур розглянутого об'єкта, тобто у визначенні залежності

T = f (x, y, z, t), (1)

де Т – температура, t – час, x. y, z - просторові координати в декартовій системі.

Температура є величина скалярна, тому температурне поле – також скалярна величина. Відзначимо, що приведене вище визначення поля справедливе і для векторних величин, що показують і величину і напрямок /сила, швидкість, прискорення та ін./. Такі поля називають векторними полями фізичних величин.

Розрізняють стаціонарне і нестаціонарне температурні поля. Нестаціонарним температурним полем називають поле, температура якого змінюється у просторі і в часі. У цьому випадку говорять, що температура є функція простору і часу. Прикладом математичного запису нестаціонарного температурного поля є рівняння (1).

Стаціонарним температурним полем називається поле, температура якого в будь-якій його точці не змінюється з часом, тобто є функцією тільки координат

T = f₁(x, y, z), 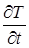= 0 (2)

Теплові режими, що характеризуються нестаціонарними температурними полями, називаються несталими. У випадку, коли температурні поля стаціонарні, теплові режими називають сталими.

Відповідно до числа просторових координат, від яких залежить температура, температурне поле може бути тривимірним (його запис має вид рівностей (1), (2), двомірним

T = f₂(x, y, t), 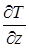= 0

і одновимірним

T = f₃(x, t),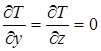

У багатьох задачах теплопровідності зручніше користуватися не декартовою, а криволінійною системою координат. У цьому випадку рівняння (1) має вигляд

T = f(x₁, x₂, x₃, t),

де х₁, х₂, х₃ – координати обраної криволінійної системи координат. Наприклад, циліндричної, сферичної та ін.

Температурний градієнт. Якщо з'єднати точки тіла, що мають однакову температуру, то одержимо поверхню рівних температур, названу ізотермічною. Ізотермічні поверхні є поверхнями рівня температурного поля й описуються рівнянням

T = f (x, y, z, t) = C, (3)

де С = const.

При перетині ізотермічної поверхні площиною одержимо сімейство ізотерм (ліній, що відповідають однаковій температурі). Якщо температурне поле неперервне, ізотермічні поверхні та ізотермічні лінії для даних температур не перетинаються між собою і не обриваються усередині нього, тому що в одній і тій же точці тіла не може бути двох різних значень температури. Розглянемо дві близькі ізотермічні поверхні з температурами Т і Т + DТ (рис.1).

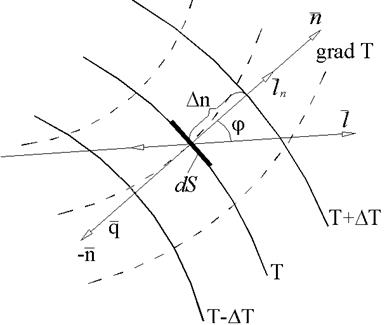
Рисунок 1– Температурне поле та його характеристики

Уздовж ізотермічної поверхні Т зміни температури не відбуваються, тому що ізотермічна поверхня – геометричне місце точок з однаковою температурою, а уздовж довільно обраного напрямку l, що перетинає ізотерму Т + DТ, спостерігається зміна температури. При цьому найбільший перепад температури на одиницю довжини буде спостерігатися при переміщенні за напрямком нормалі 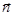до ізотермічної поверхні.

Межа відносності зміни температури DТ до відстані між ізотермами Т і Т + DТ по нормалі Dn при Dn ®0 називають градієнтом температури, тобто

|grad T |= 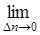( 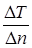) (4)

Градієнт температури є вектор, спрямований по нормалі до ізотермічної поверхні, причому за позитивний напрямок цього вектора приймається напрямок у бік зростання температури:

grad T = ( ),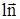

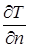де 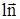– одиничний вектор нормалі до ізотермічної поверхні, спрямований убік зростання температури; 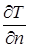- похідна від температури за напрямком нормалі n. Похідна 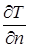в напрямку зменшення температури від’ємна. Для вектора градієнта використовується також позначення

grad T = 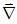Т (6)

Відповідно до позначення(6) вектор 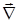у декартовій системі координат може бути представлений у такий спосіб:

,

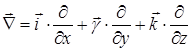
де 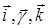- одиничні вектори обраної системи координат. Проекції вектора grad Т на осі Ох, Оy, Oz, очевидно. рівні

(grad T)_x =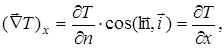

(grad T)_y =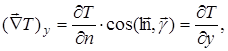

(grad T)_z =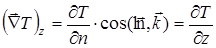

Тепловий потік. Основний закон теплопровідності Фур'є. Переніс теплоти в об’єм тіла за допомогою теплопровідності може здійснюватися тільки при неоднорідному розподілі в ньому температури, тобто необхідною умовою виникнення усередині тіла теплового потоку є відмінний від нуля градієнт температури. Відомо, що теплота передається від областей з більшою температурою до точок з меншою температурою, тому тепловий потік на відміну від температури, що є скалярною величиною, має визначений напрямок.

Позначимо повну кількість теплоти, яка пройшла через ізотермічну поверхню S за час t, через Q_t.

Тоді в одиницю часу dt через цю поверхню проходить кількість теплоти Q = 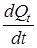, яка називається тепловим потоком.