Теорема Остроградского-Гаусса. Выделим в диэлектрике замкнутую гауссову поверхность (рис

Выделим в диэлектрике замкнутую гауссову поверхность (рис. 5.9). При однородной поляризации диэлектрика на его поверхности возникнут связанные заряды, но внутри поверхности объёмных поляризационных зарядов не будет.

Рис. 5.9.

Ситуация меняется в случае неоднородной поляризации диэлектрика, которую мы здесь не рассматриваем.

Вычислим заряд, покидающий выделенный объём через гауссову поверхность в результате поляризации (рис. 5.10):

,

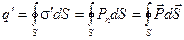где s’ — локальная поверхностная плотность поляризационных зарядов, возникших на выделенной поверхности dS.

Рис. 5.10.

q’ — заряд, покинувший объём.

Тогда внутри гауссовой поверхности возникнет поляризационный заряд:

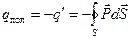. (5.14)

Сформулируем теперь теорему Остроградского-Гаусса:

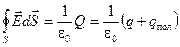. (5.15)

Заряд, определяющий поток вектора напряжённости через гауссову поверхность, в случае диэлектрика складывается из «стороннего» заряда q и заряда q_пол, возникшего в объёме в результате поляризации диэлектрика.

Воспользуемся результатом (5.14) и перепишем (5.15) ещё раз:

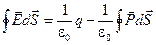
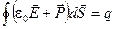
Здесь 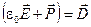(см. 5.10) — вектор электрического смещения. Значит, теорему Остроградского-Гаусса для электрического поля в диэлектрике можно сформулировать так:

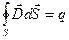. (5.16)

Поток вектора электрического смещения через любую замкнутую поверхность равен алгебраической сумме несвязанных (свободных) зарядов, заключённых внутри этой поверхности.

Ещё раз напомним, что вектор электрического смещения (индукции) связан с вектором напряжённости электрического поля (5.12):

.

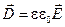Преимущество теоремы Остроградского-Гаусса в форме (5.16) состоит в том, что теперь для расчёта потока не нужно знать величину поляризационных зарядов q_пол, возникающих в диэлектрике. Поток вектора электрической индукции определяется только суммой свободных зарядов q.