Электрический ток. Характеристики электрического тока

Электрическим током называется упорядоченное движение заряженных частиц, в процессе которого происходит перенос электрического заряда.

В металлическом проводнике, например, такими частицами являются свободные электроны. Они находятся в постоянном тепловом движении. Это движение происходит с высокой средней скоростью, но в силу его хаотичности не сопровождается переносом заряда. Выделим мысленно в проводнике элемент поверхности dS: за любой промежуток времени число электронов преодолевших эту поверхность слева направо будет в точности равно числу частиц прошедших через эту поверхность в обратном направлении. Поэтому заряд, перенесённый через эту поверхность, окажется равным нулю.

Ситуация изменится, если в проводнике появится электрическое поле. Теперь носители заряда будут участвовать не только в тепловом, но и в упорядоченном, направленном движении. Положительно заряженные носители будут двигаться по направлению поля, а отрицательные — в противоположном направлении.

В общем случае в переносе заряда могут принимать участие носители обоих знаков (например, положительные и отрицательные ионы в электролите).

Скорость движения таких частиц будет складываться из скорости их теплового 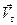и направленного 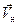движений:

.

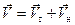Среднее значение скорости частиц оказывается равным средней скорости направленного движения:

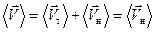
Хаотичность теплового движения приводит к тому, что среднее значение вектора скорости этого движения равно нулю 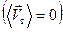. Ещё раз подчеркнём, что речь идёт о среднем значении вектора, но не модуля скорости теплового движения заряженных частиц.

Основной количественной характеристикой электрического тока является сила тока. Сила тока в проводнике численно равна величине заряда, переносимого через полное сечение проводника в единицу времени:

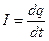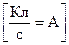, . (6.1)

Сила тока в системе СИ измеряется в амперах. Это скалярная характеристика. Сила тока может быть как положительной, так и отрицательной. Если направление тока совпадает с условно принятым положительным направлением вдоль проводника, то сила такого тока I > 0. В противном случае сила тока отрицательна.

Часто за положительное направление вдоль проводника принимается направление, в котором перемещаются (или перемещались бы) положительные носители заряда.

Второй важной характеристикой электрического тока является плотность тока. Выделим мысленно в проводнике поверхность DS, перпендикулярную скорости направленного движения 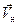носителей заряда. Построим на этой поверхности параллелепипед с высотой, численно равной скорости V_н (рис. 6.1.). Все частицы, находящиеся внутри этого параллелепипеда за одну секунду пройдут через поверхность DS. Число таких частиц:

,

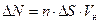где n — концентрация частиц, то есть число частиц в единице объёма. Заряд, который будет пронесён этими частицами через поверхность DS, определит силу тока:

.

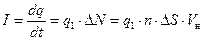Здесь q₁ — заряд одного носителя. Разделив силу тока на площадь сечения DS, получим заряд, который протекает за единицу времени через поверхность единичной площади. Это и есть плотность тока:

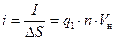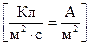, . (6.2)

Рис. 6.1.

Поскольку скорость направленного движения заряженных частиц — векторная величина, это выражение записывают в векторном виде:

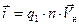. (6.3)

Уменьшая площадку DS, приходим к локальной характеристике электрического тока — к плотности тока в точке:

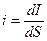(6.4)

Это модуль плотности тока, а направление вектора плотности тока в данной точке совпадает с направлением скорости движения частиц 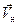, или с направлением напряжённости электрического поля 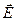в данной точке. Силу тока, протекающего через элементарную площадку dS теперь можно записать в виде скалярного произведения двух векторов (рис. 6.2.):

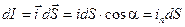. (6.5)

Для того, чтобы вычислить силу тока через сечение S, нужно просуммировать все токи, протекающие через элементы этого сечения, то есть взять интеграл:

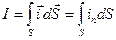. (6.6)

Интеграл 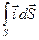представляет собой поток вектора плотности тока 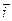, поэтому две основные характеристики электрического тока связывают иногда такой легко запоминающейся фразой: сила тока равна потоку вектора плотности тока.

Рис. 6.2.

Продолжим разговор о потоке вектора 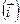. Теперь в проводящей среде выделим замкнутую поверхность S (рис. 6.3.). Если известен вектор плотности тока в каждой точке этой поверхности, то легко вычислить заряд, покидающий объём, ограниченный этой поверхностью, в единицу времени:

.

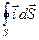Рис. 6.3.

Пусть внутри поверхности S находится заряд q, тогда за единицу времени Dt = 1 он уменьшится на величину 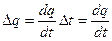. Изменение заряда связано с его истечением из объёма, то есть:

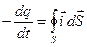. (6.7)

Это уравнение называется уравнением непрерывности. Оно представляет собой математическую запись закона сохранения электрического заряда.