Преобразование Тастина
Это преобразование позволяет получить дискретную передаточную функцию линейного объекта из его исходной непрерывной передаточной функции:
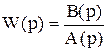
При малом шаге квантования справедлива следующая замена переменной:
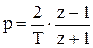
Обоснования.
1.Запишем аналитическую выражение, связывающее операторы «p» и «z», а затем разложим логарифм в ряд Тейлора:
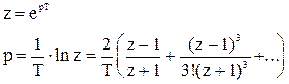 .
.
В последнем выражении отбросим все члены ряда кроме первого.
2. Воспользуемся методом трапеций для аппроксимации процедуры интегрирования (рис.1.21).
|
Рис. 1.21
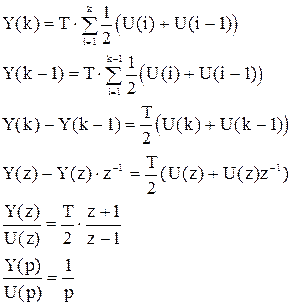
Дата добавления: 2015-08-04; просмотров: 3662;
