Экспериментальное получение характеристик случайного процесса.
1. Эргодические СП.
2. Оценка КФ.
3. Оценка спектральной плотности.
Пусть имеется СП  . Для полного описания его, необходимо найти ФР этого процесса, то есть
. Для полного описания его, необходимо найти ФР этого процесса, то есть 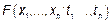 . Однако нахождение
. Однако нахождение 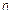 -мерной ФР представляется неразрешимой задачей. Поэтому для его описания используют менее информативные вероятностные характеристики:
-мерной ФР представляется неразрешимой задачей. Поэтому для его описания используют менее информативные вероятностные характеристики: 
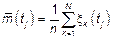
В общем случае
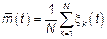 , где
, где  – СПы (независимые), характеристики которых совпадают с характеристиками исходного СП.
– СПы (независимые), характеристики которых совпадают с характеристиками исходного СП.
 (х)
(х)
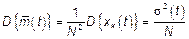 (хх)
(хх)
Для использования этих формул необходимо обладать большим набором реализаций  .
.
Предположим, что  – ССП:
– ССП:
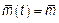 .
.
Таким образом формулы (х) и (хх) являются общими для стационарных и нестационарных СП.
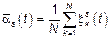 .
.
Рассмотрим ССП. Для него: 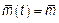 – постоянная составляющая СП
– постоянная составляющая СП  .
.
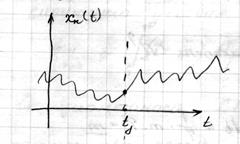
Предположим имеется реализация  . Как определить постоянную составляющую?
. Как определить постоянную составляющую?
Для детерминированной функции (непериодической) 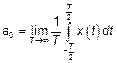
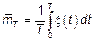 – может ли быть эта формула оценкой МО по одной реализации?
– может ли быть эта формула оценкой МО по одной реализации?
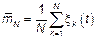 – по набору реализаций.
– по набору реализаций.
 тогда
тогда  .
.
Тогда при 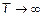 и
и 
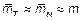 .
.
ССП  называется эргодическим, если его среднее по ансамблю реализаций совпадает со средним по одной реализации.
называется эргодическим, если его среднее по ансамблю реализаций совпадает со средним по одной реализации.
Возникает вопрос, а как проверить свойства эргодичности СП?
Необходимо проверить свойства оценки 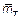
1)  – данная оценка является несмещенной.
– данная оценка является несмещенной.
2) 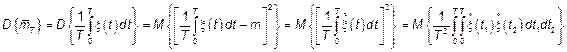
 .
.
Поскольку, при 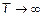
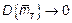 , то оценка является состоятельной.
, то оценка является состоятельной.
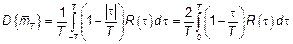 .
.
Таким образом процесс  будет эргодическим если его корреляционная функция удовлетворяет следующему условию (необходимо и достаточно).
будет эргодическим если его корреляционная функция удовлетворяет следующему условию (необходимо и достаточно).
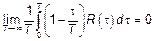 .
.
Достаточным является условие 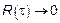 при
при 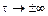 .
.
Достаточно стационарности в широком смысле.
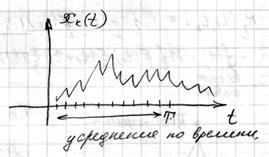
| Эргодичность, которую мы сформулировали называется эргодичностью относительно МО.
Не все ССП являются эргодическими.
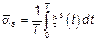 1)
1) 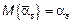 – несмещенная оценка.
2) – несмещенная оценка.
2) 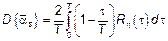 , где , где 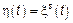 . .
|
ССП эргодичен относительно моментов 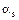 при выполнении следующего условия:
при выполнении следующего условия:
 .
.
Стационарность СП в широком смысле уже не удовлетворительна, потому при рассмотрении моментов более высокого порядка необходимо, чтобы процесс был стационарным в узком смысле.
 – ССП в узком смысле.
– ССП в узком смысле.
Процесс наблюдается на конечном интервале
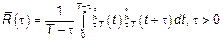 (1)
(1)
1) Существуют формулы с 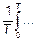
2) 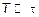
 Таким образом
Таким образом 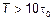
В формуле (1) при центрировании можно использовать либо 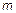 , либо
, либо 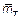 (во втором случае формулы для ошибок намного усложняются).
(во втором случае формулы для ошибок намного усложняются).
На практике предполагают, что  .
.
1) Оценка 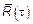 является несмещенной.
является несмещенной.
2) 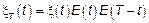
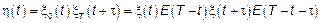
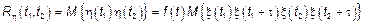
Таким образом корреляционные функции на хвостах производятся с очень большой относительной ошибкой.
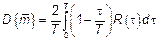
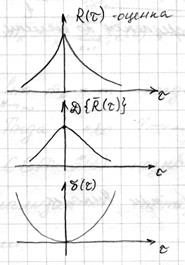 
| Для улучшения качества оценки корреляционной функции  , где , где  – корреляционное окно, которое должно удовлетворять всем свойствам корреляционной функции. В литературе рассмотрены не менее 10 корреляционных окон. – корреляционное окно, которое должно удовлетворять всем свойствам корреляционной функции. В литературе рассмотрены не менее 10 корреляционных окон.
|
Дата добавления: 2015-08-04; просмотров: 596;
