СП с дискретным спектром
1. Спектры детерминированных процессов.
2. Гармоника со случайными параметрами.
3. СП с дискретным спектром.
В книгах встречается следующее определение спектра СП
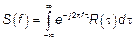 и соответственно
и соответственно 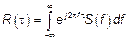
Возникает ряд вопросов: а почему 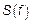 находится с помощью
находится с помощью 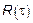 ; почему используется преобразование Фурье и т. д.
; почему используется преобразование Фурье и т. д.
Если есть  , обладающее свойством
, обладающее свойством 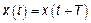 , тогда:
, тогда:
1) 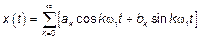 ,
, 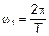
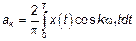 ,
, 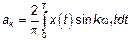
Инженеры используют вторую формулу представляя
2) 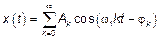 ,
, 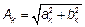 ,
, 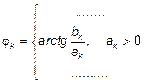
3) 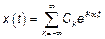 ,
, 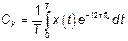
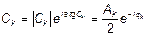
Можем ли мы использовать все выше приведенные формулы для анализа спектра ССП  ?
?
Напрямую ряд Фурье не применим так как ССП не обладает свойствами периодичности.
1.2) 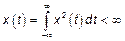 тогда
тогда 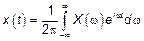 ,
, 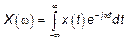 .
.
Вопрос: Является ли ССП сигналом с конечной энергией? – Нет 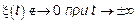 , то есть не обладает конечной энергией.
, то есть не обладает конечной энергией.
Пуст  – ССП в широком смысле.
– ССП в широком смысле.
2.1. 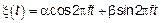 ,
, 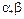 – СВ.
– СВ.
Каким условиям должны удовлетворять 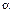 и
и 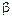 чтобы
чтобы  был ССП.
был ССП.
1) 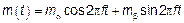
2) 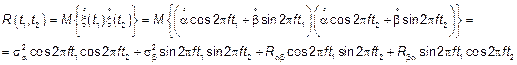
Условия: 1) 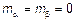
2) 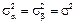
3) 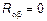
При этих условиях: 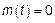 ,
, 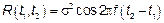
2.2. 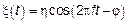 ,
, 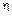 ,
, 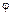 – независимые СВ,
– независимые СВ, 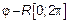
Запишем исходный процесс в следующем виде
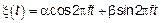 ,
, 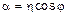 ,
, 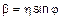 .
.
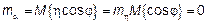
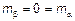
Д.з. показать, что 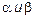 – некоррелированны и найти дисперсию
– некоррелированны и найти дисперсию  .
.
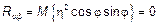
Таким образом накладывать условия на величины 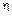 и
и 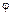 нет необходимости
нет необходимости 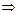
 – ССП
– ССП
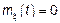
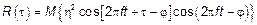
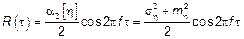 .
.
Пусть: 1) 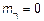
2) 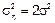
Таким образом для данной модели с учетом последних замечаний
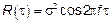
2.3. 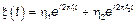
Такой процесс, в общем случае, является комплексным СП. Тогда, пусть 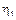 и
и 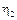 – комплексные СВ.
– комплексные СВ.
Запишем МО процесса  :
:
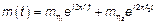
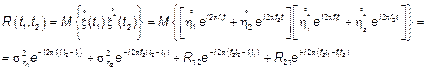
Для того, чтобы  был ССП необходимо:
был ССП необходимо:
1) 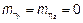
2) 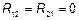
Тогда корреляционная функция СП  будет иметь вид
будет иметь вид
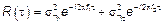
Введем следующие обозначения
1) 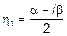 ,
, 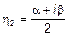 – комплексно сопряженные пары.
– комплексно сопряженные пары.
2) 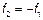
Подставим в модель 2.3.
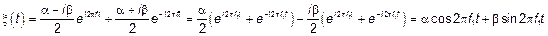
Тогда 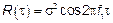
3.1 
Ограничения: все 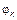 – независимы и имеют
– независимы и имеют 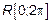
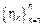 :
: 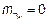 ,
, 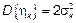 ,
, 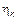 – некоррелированна.
– некоррелированна.
Все 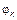 ,
, 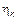 – независимые. Тогда характеристики СП
– независимые. Тогда характеристики СП  будут равны:
будут равны:
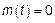
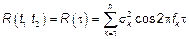
Таким образом СП  является стационарным в широком смысле.
является стационарным в широком смысле.
Вопрос: можно ли 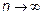
Вспомним, что 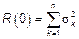 тогда, если
тогда, если 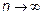 необходимо
необходимо 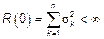
СП  можно представить в виде бесконечной сумы гармоник со случайными амплитудами и начальными фазами, тогда
можно представить в виде бесконечной сумы гармоник со случайными амплитудами и начальными фазами, тогда 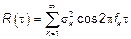 , где амплитудный множитель перед косинусом представляет собой дисперсию амплитуды.
, где амплитудный множитель перед косинусом представляет собой дисперсию амплитуды.
При этом дисперсия процесса равна суме дисперсий амплитуд гармоник.
Дискретным спектром процесса является набор 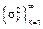 амплитуд гармонических составляющих на которые раскладывается ССП
амплитуд гармонических составляющих на которые раскладывается ССП  .
.

Проведем аналогию с радом Фурье. 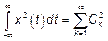
3.2. 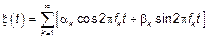 –данная модель является общей, так как в частном случае мы можем задать
–данная модель является общей, так как в частном случае мы можем задать 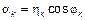 и
и 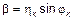
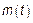 и
и 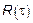 модели 3.2 совпадают с
модели 3.2 совпадают с 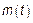 и
и 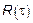 модели 3.1.
модели 3.1.
3.3. Если 1) 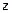 – комплексное число, тогда
– комплексное число, тогда 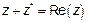
2) 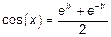
Введем комплексно сопряженные пары:
1) 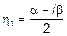 ,
, 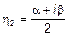
2)
Тогда СП  можно записать в следующем виде:
можно записать в следующем виде:
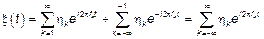
Вводим СВ 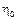 :
: 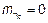 ;
; 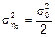 ;
; 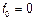
Данный процесс является действительным.
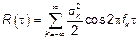
Отметим частные случаи:
Пусть 
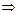
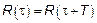 то есть функция периодическая, то есть
то есть функция периодическая, то есть 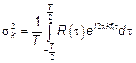
Дата добавления: 2015-08-04; просмотров: 719;
