Простейшие преобразования СП
1.1 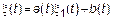 ,
,
где 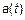 ,
, 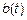 – детерменированние функции;
– детерменированние функции; 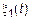 – СП.
– СП.
Все последующие задачи будем рассматривать в рамках корреляционной теории.
Найдем математическое ожидание (МО) процесса 
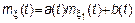

Найдем 
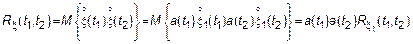
Таким образом 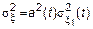
Возникает вопрос может ли быть процесс  стационарным случайным процессом (ССП)?
стационарным случайным процессом (ССП)?
1) МО в общем случае не равно const. В частности, когда 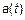 ,
, 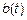
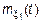 – const, тогда
– const, тогда 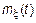 – const.
– const.
Возможно, что 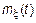 – const при
– const при 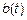 – const и
– const и 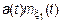 – const.
– const.
2) В общем случае данный процесс является нестационарным
1.2.  (линейная комбинация СП)
(линейная комбинация СП)
1. 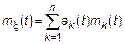
2. 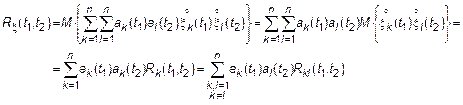
Частный случай, если все  и входящие в сумму процессы некоррелированы корреляционная функция суммы равна сумме корреляционных функций
и входящие в сумму процессы некоррелированы корреляционная функция суммы равна сумме корреляционных функций
Процесс такого вида является нестационарным, однако при 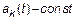 и процессы
и процессы 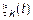 – стационарно связанные.
– стационарно связанные.
3. Пусть все 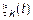 – некоррелированы
– некоррелированы
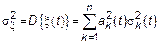 .
.
Если сумма бесконечна имеет ли смысл рассматривать процесс  ? Когда
? Когда 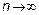 необходимо потребовать, чтобы
необходимо потребовать, чтобы 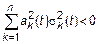 (Так как в рамках корреляционной теории дисперсия должна быть конечной).
(Так как в рамках корреляционной теории дисперсия должна быть конечной).
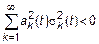 , разложения СП
, разложения СП
Каноническое разложение СП (один из видов)
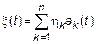 (другой вариант), где
(другой вариант), где  – детерминированная функция,
– детерминированная функция, 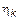 – случайная величина (СВ).
– случайная величина (СВ).
Эти канонические разложения ввел академик Пугачев (в его книге описано получения этих канонических разложений).
Функции  и
и 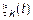 называются координатными функциями в канонических разложениях.
называются координатными функциями в канонических разложениях.
1.3. 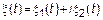 ,
, 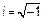
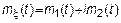

Модуль возникает из-за физического смысла 
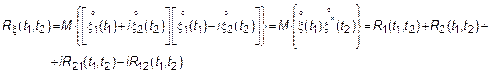
Если действительная и мнимая часть некоррелированы, то  – действительная функция. Таким образом если
– действительная функция. Таким образом если  – действительная, то это не значит, что сам процесс действителен. Процесс будет стационарен, если Re и Im являются стационарно свзанными. Комплексный СП
– действительная, то это не значит, что сам процесс действителен. Процесс будет стационарен, если Re и Im являются стационарно свзанными. Комплексный СП  называется гильбертовым если он обладает конечной дисперсией, то есть
называется гильбертовым если он обладает конечной дисперсией, то есть 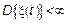 (Аналогия с ТПС, конечная средняя мощность или процессы с конечной энергией).
(Аналогия с ТПС, конечная средняя мощность или процессы с конечной энергией).
Дисперсия характеризует не только размах значений, с точки зрения энергии она характеризует среднюю мощность СП.
Функция 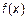 непрерывна в точке
непрерывна в точке 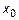 , когда
, когда

Последовательность 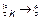 если
если
Для СВ существует 4 вида сходимости
1. с вероятностью 1
2. по вероятности
3. среднеквадратическая
4. по распределению
Распишем среднеквадратическую метрику
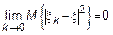
Возникает необходимость в решении предела, что является проблематично. Как уйти от предела? Лоэв решил эту проблему, предложив критерий, названый в его честь.
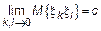 тогда
тогда 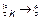
Определение СП  называется непрерывным при
называется непрерывным при 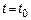 если
если
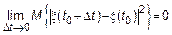 (1.1)
(1.1)
Целью является определение свойств МО,  через существование (1.1)
через существование (1.1)
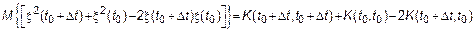
Если 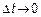 то
то  в этой точке
в этой точке  – непрерывной и по диагонали
– непрерывной и по диагонали
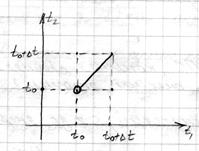
| если  непрерывна в любой точке непрерывна в любой точке 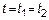 то процесс называется непрерывным.
Этот процесс стохастически непрерывным
1) то процесс называется непрерывным.
Этот процесс стохастически непрерывным
1) 
 – непрерывна на диагонали, то есть при – непрерывна на диагонали, то есть при 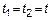 ( ( 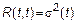 ) )
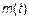 – тоже должна быть непрерывна (по свойствам непрерывных функций). – тоже должна быть непрерывна (по свойствам непрерывных функций).
|
Таким образом для непрерывности СП необходимо, чтобы непрерывна была  и
и 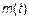 .
.
1.2)  – ССП (условие непрерывности для
– ССП (условие непрерывности для 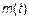 не нужно, так как
не нужно, так как 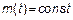 )
)
только 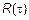 при
при 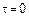 определяет непрерывность СП
определяет непрерывность СП
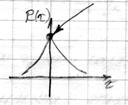
1.3) Из того, что  является непрерывным не следует что его реализации являются непрерывными функциями.
является непрерывным не следует что его реализации являются непрерывными функциями.

Пусть все реализации СП кусочно-постоянные, то есть имеют разрыв второго рода.
Такой процесс является непрерывным если точки 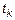 не являются фиксированными.
не являются фиксированными.
Если 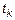 – не фиксированные, то точки
– не фиксированные, то точки 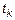 случайным образом расположены на временной оси.
случайным образом расположены на временной оси.
Пример
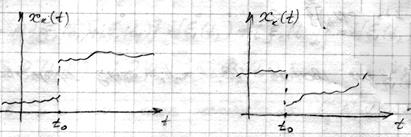
Процесс не является непрерывным так как его реализации имеют разрыв (всегда) в момент времени 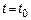 .
.
У случайного процесса доминирующими являются не реализации, а его вероятностные свойства.
Определение: Пусть 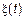 – непрерывный СП, тогда СП
– непрерывный СП, тогда СП 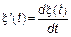 называется производной процесса
называется производной процесса 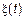
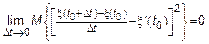
Воспользуемся критерием Лоэва для объяснения условий, которым должна удовлетворять 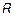 и МО.
и МО.
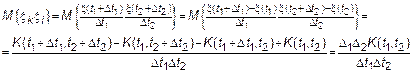
Вычислим предел вида
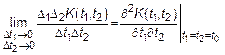
Для того, чтобы СП 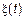 был дифференцирован в точке
был дифференцирован в точке 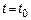 необходимо и достаточно чтобы в этой точке была дифференцируемая его ковариационная функция.
необходимо и достаточно чтобы в этой точке была дифференцируемая его ковариационная функция.
1. Если  дифференцируемая в любой точке
дифференцируемая в любой точке 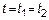 , то процесс дифференцируемый на всей временной оси.
, то процесс дифференцируемый на всей временной оси.
Вычислим условие которое должна удовлетворять  и МО дифференцируемого СП.
и МО дифференцируемого СП.

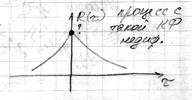 2. Следовательно
2. Следовательно 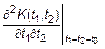 и
и 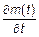 должна существовать.
должна существовать.
3. 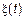 – ССП.
– ССП.

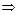
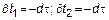
4. Если СП является дифференцируемым, то это не значит, что дифференцируемыми являются его реализации.
Пусть 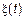 – комплексный СП.
– комплексный СП.
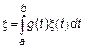 , где
, где 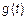 – комплекснозначная функция.
– комплекснозначная функция.
Необходимо узнать условия которым должны удовлетворять характеристики СП 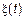 , чтобы этот интеграл существовал или имел смысл.
, чтобы этот интеграл существовал или имел смысл.
Разбив промежуток времени 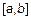 на точки
на точки 
 ,
, 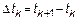
Если предел при 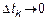
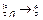 то тогда мы говорим, что существует интеграл от СП.
то тогда мы говорим, что существует интеграл от СП.
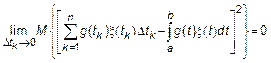
Согласно критерию Лоэва:

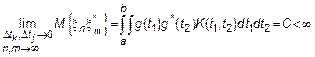
Если при 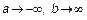 предел существует, то СП
предел существует, то СП 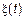 – интегрируем. Мы рассмотрим интеграл вида
– интегрируем. Мы рассмотрим интеграл вида 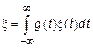 , однако часто необходимо рассматривать
, однако часто необходимо рассматривать 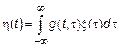
Условие существования такого интеграла
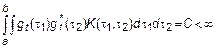
Если 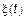 – ССП все тоже самое, только
– ССП все тоже самое, только 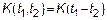
Если весовая функция 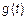 является спадающей, то ее наличие упрощает требования к ковариационной функции
является спадающей, то ее наличие упрощает требования к ковариационной функции  .
.
Корреляционный анализ линейных систем (ЛС)
1. Анализ параметрических ЛС.
2. Анализ непараметрических ЛС.
3. Анализ многокаскадных ЛС.
4. Линейные случайные процессы.
Вспомним: если есть 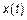 , отклик
, отклик 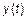 и оператор
и оператор 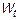 , то тогда между ними существует следующая связь
, то тогда между ними существует следующая связь
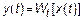
Классификация систем была приведена в курсе ТПС.
Линейная система – это система, которая удовлетворяет принципу суперпозиции. 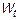 в этом случае обозначается
в этом случае обозначается  .
.
Временная область: 1) дифференциальные уравнения
2) импульсная переходная функция (ИПФ)
По сути ИПФ является решением дифференциального уравнения. Эти характеристики практически всегда можно получить одну через другую.
Дифференциальные уравнения не дают связи между 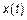 и
и 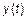 .
.
ИПФ напрямую дает связь между 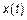 и
и 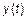 .
.
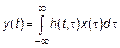 , где
, где  – отклик ЛС на
– отклик ЛС на 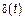 .
.
Для непараметрических систем (характеристики не зависят от  )
)
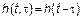
Заданы: вероятностные характеристики воздействия, 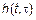 и требуется найти вероятностные характеристики отклика.
и требуется найти вероятностные характеристики отклика.
Данная задача может быть решена в полной постановке (в узком смысле – в терминологии закона распределения (ЗР)) или в широком смысле – корреляционная теория. Нахождение ЗР отклика на выходе ЛС в настоящее время отсутствует за исключением нескольких частных случаев.
Мы будем решать эту задачу в рамках корреляционной теории.
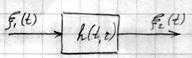
Необходимо найти: 1) 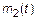 ; 2)
; 2) 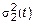 ; 3)
; 3) 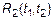 ; 4)
; 4) 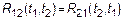
Используя свойство МО найдем вышеперечисленные характеристики.
1) 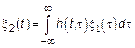
2) 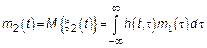
3) 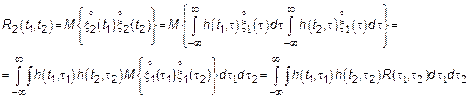
где 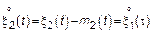
Для существования 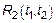 необходимо интегрирование МО и корреляционной функции с весом.
необходимо интегрирование МО и корреляционной функции с весом.
5) 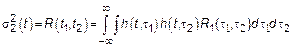
6) 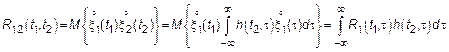
Можно ли говорить (на основании полученных результатов), что  – ССП (при общей постановке задачи).
– ССП (при общей постановке задачи).
В общем случае  – нестационарный СП.
– нестационарный СП.
При каких условиях  может быть ССП.
может быть ССП.
1) Пусть система является непараметрической
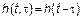
2) Воздействие – ССП
Для решения задачи мы будем использовать полученные ранее формулы
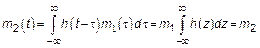
Таким образом система пассивна – МО воздействия и отклика совпадают.
Пассивная система – это система, в которой отсутствуют устройства преобразования энергии.

Произведем замену  ,
,  ,
,  .
.

Таким образом процесс  является стационарным (корреляционная функция зависит от разности
является стационарным (корреляционная функция зависит от разности  )
)
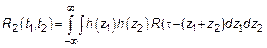
Замена 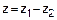 ,
, 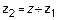 ,
, 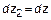 .
.
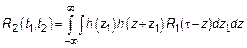
 – Корреляционное преобразование системы
– Корреляционное преобразование системы
 . Окончательное выражение для нахождения
. Окончательное выражение для нахождения 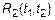
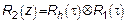
 .
.
Результирующая формула
 .
.
Проверим, как ведет себя взаимная корреляционная функция
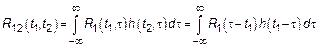
Замена 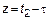 ,
,  ,
,  ,
,
в результате замены получим:
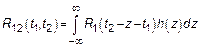 .
.
Таким образом воздействие и отклик являются стационарно связанными СП.
 .
.
Самостоятельно 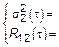
3.1 Последовательная система
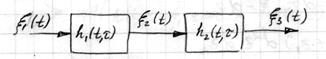

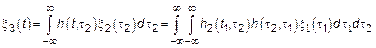
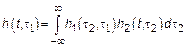
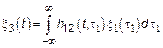
Таким образом задача может быть сформулирована несколько иначе
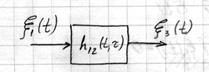 таким образом
таким образом 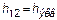
Если система является непараметрической то эквивалентная система тоже является непараметрической и определяется:
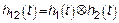
Выводы: Все результаты, полученные в пп. 1,2 справедливы для последовательной системы. Количество систем в цепочке неважно.
3.2. Параллельные системы
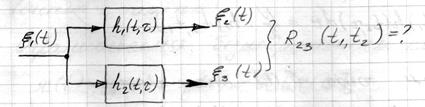
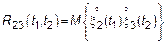
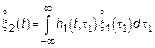
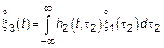

Когда характеристики системы совпадают, то 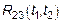 совпадает с корреляционными функциями
совпадает с корреляционными функциями
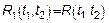
Дальнейший анализ: можно предположить, что будет если обе системы непараметрические и воздействие является ССП
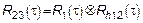
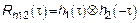
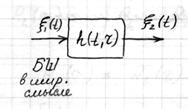
На вход подается белый шум (БШ) в широком смысле, так как задача решается в рамках корреляционной теории.
Рассмотрим стационарный БШ.
Предположим, что 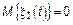
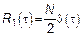 ,
, 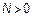 – интенсивность БШ.
– интенсивность БШ.
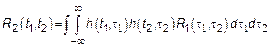
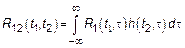 ; Для стационарного БШ получим
; Для стационарного БШ получим

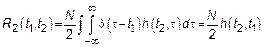
Если система непараметрическая, тогда 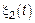 – стационарный процесс.
– стационарный процесс.
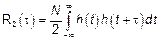 ,
, 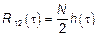
 с точностью до постоянной совпадает с корреляционным преобразованием системы.
с точностью до постоянной совпадает с корреляционным преобразованием системы.
 с точностью до постоянной совпадает с импульсной переходной функцией
с точностью до постоянной совпадает с импульсной переходной функцией
 – часто используется при идентификации системы.
– часто используется при идентификации системы.
Вспомним, что
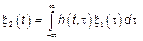 , в том случае, когда
, в том случае, когда  – БШ – процесс
– БШ – процесс  называют линейным СП (ЛСП).
называют линейным СП (ЛСП).
В узком смысле в узком смысле
В широком смысле в широком смысле
ЛСП – это отклик системы при воздействии на нее БШ.
Возникает ряд задач:
1) Если БШ в узком смысле, то что тогда будет? Нахождение ЗР.
2) Каким образом ЛСП можно представить как результат фильтрации БШ линейной системой с ИПФ  ? Обратная задача. Задача заключается в нахождении
? Обратная задача. Задача заключается в нахождении  , тогда этот фильтр называют формирующим фильтром.
, тогда этот фильтр называют формирующим фильтром.
ЛСП в узком смысле мы рассмотрим позднее.
Дата добавления: 2015-08-04; просмотров: 856;
