Точечное оценивание вероятностных характеристик случайных величин.
1. Точечные оценки.
2. Оценки ЗР.
3. Оценки моментов.

Если имеется  и имеется ее ФР
и имеется ее ФР 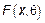
1) Известно распределение но 
2) 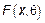 – ?
– ?
Задача тогда заключается в следующем: проводим  раз измерение, в результате получаем
раз измерение, в результате получаем  .
.
1) Необходимо найти оценку  ,
, 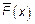 .
.
2) Ошибки.
В первом эксперименте получим 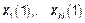
Во втором 
В к-ом 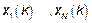
Вопрос: а чему равно 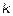 ?
?
 Тогда моделью эксперимента является вектор
Тогда моделью эксперимента является вектор 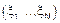 с областью возможных значений
с областью возможных значений  ,
,  – реализация случайной выборки.
– реализация случайной выборки.
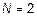 , нас интересует
, нас интересует  , а получаем
, а получаем 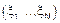
1)  – функциональное преобразование случайной величины
– функциональное преобразование случайной величины 
2) 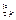 – могут быть зависимы.
– могут быть зависимы.
Вероятностные характеристики случайной выборки: 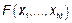 , но это довольно сложно.
, но это довольно сложно.
Тогда предполагаем, что ЗР 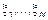 – одинаковы и совпадают с ЗР СВ
– одинаковы и совпадают с ЗР СВ  .
.
Этим предположением мы не учитываем влияние среды и аппаратуры. 2) Считают, что все 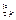 – независимы.
– независимы.
На основании этих предположений можно записать
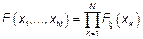
Если известна ФР но не знаем  – параметрические методы.
– параметрические методы.
Если мы не знаем ФР – непараметрический метод (хуже изучен).
Если  – параметр (
– параметр ( 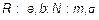 ) точечной оценкой
) точечной оценкой  называется любая функция от результатов наблюдения,
называется любая функция от результатов наблюдения, 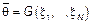 , где
, где 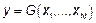 .
.
Почти не различны термины «статистика» и «оценка».
Задача сводится к нахождению 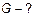 .
.
1. Метод максимального правдоподобия – параметрический метод.
2. Метод моментов – непараметрический метод.
3. Метод наименьших квадратов.
Предположим, что получили оценку 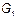 ,
, 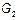 и соответственно
и соответственно  и
и 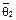 .
.
Вопрос: а какую выбрать?
Для выбора соответствующей оценки необходимо проверить свойства этой оценки. Свойства основаны на том, что  – СВ.
– СВ.
Тогда для нее есть 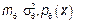

Основными свойствами оценки являются:
– несмещенность;
– состоятельность;
– эффективность;
1) Оценка называется несмещенной, если 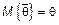 , если оценка смещенная, то смещение определяется как
, если оценка смещенная, то смещение определяется как  .
.
Если при  ,
, 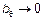 то оценка называется ассимптотичной несмещенной.
то оценка называется ассимптотичной несмещенной.
2) Оценка называется состоятельной, если она стремится к теоретическому параметру по вероятности.
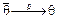 или
или 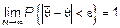 , при
, при 
В общем случае необходимо знать ЗР оценки.
Согласно Чебышеву 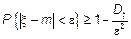 , если
, если 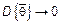 при
при  , то оценка состоятельна.
, то оценка состоятельна.
3) Пусть построили ряд оценок 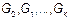 – все они состоятельны и несмещенные при конечном
– все они состоятельны и несмещенные при конечном  , то какую оценку выбрать?
, то какую оценку выбрать?
Если 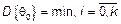 , то такая оценка называется эффективной. Существует ли вообще эффективная оценка? А если существует, то по какой формуле брать
, то такая оценка называется эффективной. Существует ли вообще эффективная оценка? А если существует, то по какой формуле брать 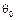 ?
?
Для ответа на этот вопрос необходимо использовать неравенство Рао-Крамера.
4) Ошибки измерения
Если введем 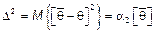
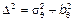
 Если
Если 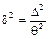 – относительная ошибка. Все вышеперечисленные оценки называются точечными, так как
– относительная ошибка. Все вышеперечисленные оценки называются точечными, так как 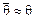 .
.
Бывают оценки и интервальные 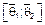 – доверительный интервал.
– доверительный интервал.
Необходимо найти доверительный интервал, который с наперед заданной 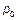 вероятностью
вероятностью 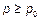 накрывал неизвестный параметр.
накрывал неизвестный параметр.
Интервал оценки применим при малом числе наблюдений 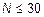 , при
, при 
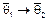 . Обычно
. Обычно 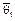 и
и  получают на базе точечных оценок.
получают на базе точечных оценок.
2.1 Как оценить вероятность появления СВ, то есть 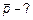
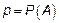 ,
, 
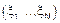 .
.
Оценкой вероятностных характеристик является частота исхода 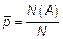 .
.
Закон распределения СВ 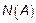 – биномиальное распределений (схема Бернулли).
– биномиальное распределений (схема Бернулли).

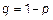 .
.
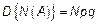
1)  – оценка несмещенная.
– оценка несмещенная.
2) 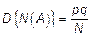 – оценка состоятельна.
– оценка состоятельна.
3)  , таким образом дисперсии СВ выражается через значения искомой СВ.
, таким образом дисперсии СВ выражается через значения искомой СВ.

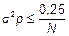
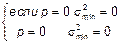


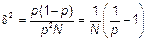
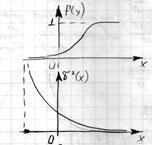
Нижний график для инженера является боле информативным, так как по верхнему графику вероятностям 0 и 1 соответствуют одинаковые значения  , а относительная ошибка существенно ??????????.
, а относительная ошибка существенно ??????????.
 2.2 Функция распределения
2.2 Функция распределения 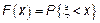
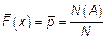 ,
,  .
.

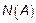 – количество элементов выборки, которые оказались левее точки
– количество элементов выборки, которые оказались левее точки  . Для реальных вычислений выборку упорядочивают по возрастанию
. Для реальных вычислений выборку упорядочивают по возрастанию 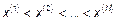 – вариационный ряд.
– вариационный ряд.
 Формула для оценки ФР.
Формула для оценки ФР.
Таким образом 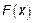 является случайной, нестационарной, стахостически непрерывной.
является случайной, нестационарной, стахостически непрерывной.
Для того, чтобы установить, является ли функция дифференцируемой необходимо знать ее корреляционную функцию 
Существенным является то, что 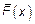 не всегда будет иметь описанный ранее вид. Однако в случае непрерывной СВ
не всегда будет иметь описанный ранее вид. Однако в случае непрерывной СВ 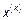 функция
функция 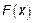 не является стохастически непрерывной.
не является стохастически непрерывной.

| 1) 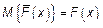 2)
2) 
 Для определения
Для определения 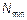 необходимо привязываться к значениям СВ необходимо привязываться к значениям СВ  .
Реализации .
Реализации 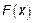 будут иметь вид. будут иметь вид.
|
2.3. Плотность вероятностей.



 , где
, где 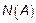 – число элементов выборки, которые попали в интервал
– число элементов выборки, которые попали в интервал 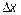 .
.
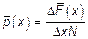 ,
, 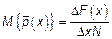 – оценка является смещенной.
– оценка является смещенной.
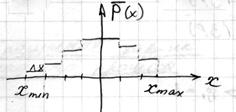
| Условно оценку плотности вероятностей можно изобразить:
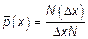 . .
|
Есть ряд наблюдений
1) Находим 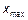 и
и 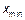 .
.
2) 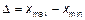 – размах варьирования.
– размах варьирования.
3) 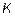 – число разбиений
– число разбиений 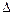 .
.
4) Определяем 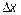 или
или 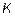 .
.
5) Находим 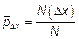 .
.
6) 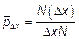 – гистограмма.
– гистограмма.
Часто под гистограммой подразумевают 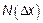 или
или 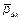 .У гистограммы точки по оси
.У гистограммы точки по оси  являются случайными, и по оси
являются случайными, и по оси 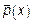 – тоже случайны.
– тоже случайны.
Качество оценки определяется тем, что получая гистограмму нужно учитывать весь возможный набор выборок.
Ряд формул, по которым можно выбирать 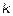 .
.

Обычно  тыс.
тыс. 
 .
.
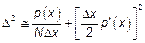 .
.
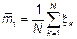 , где
, где 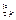 – элемент случайной выборки
– элемент случайной выборки 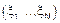
Оценка несмещенная и состоятельна.
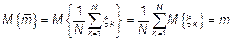 – несмещенная.
– несмещенная.
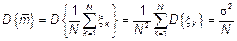 – оценка состоятельная.
– оценка состоятельная.
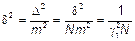 .
.
Для 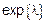 (ЗР)
(ЗР)

Для вычислений, на основании последнего примера, лучше использовать  , а не находить дисперсию оценки, так как для ряда ЗР
, а не находить дисперсию оценки, так как для ряда ЗР 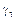 является константой.
является константой.
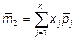 , где
, где 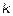 – число интервалов;
– число интервалов;  – произвольная точка, взятая внутри интервала;
– произвольная точка, взятая внутри интервала; 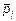 – частоты.
– частоты.
Оценка  всегда смещенная, состоятельная, не эффективная.
всегда смещенная, состоятельная, не эффективная.
Оценка дисперсии.
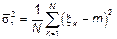 – самая хорошая ошибка (несмещенная, состоятельная).
– самая хорошая ошибка (несмещенная, состоятельная).

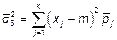
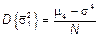
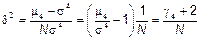 .
.
Для 
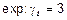
Для флуктуационных процессов все кумулянтные коэффициенты рассчитываются достаточно просто.
Если процесс стационарен
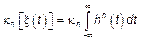
Оценка начальных моментов порядка 
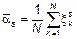 , свойства этих моментов для
, свойства этих моментов для 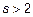 не исследованы.
не исследованы.
Дата добавления: 2015-08-04; просмотров: 767;
