Модели флуктуационных процессов
1. Процессы Бунимовича-Райса.
2. Пуассоновские импульсные процессы.
3. Линейные СП.
4. ЗР флуктуационных процессов.
Предположения
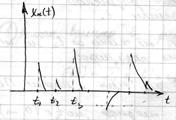
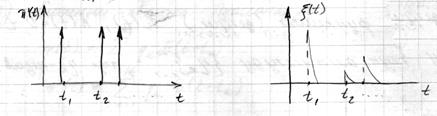
1) В случайные моменты времени 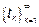 возникают элементарные импульсы.
возникают элементарные импульсы.
2) Форма импульса описывается детерминированной функцией  ,
, 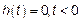
3) Импульсы имеют случайную амплитуду 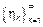 , где
, где  – независимая СВ, и независимая с
– независимая СВ, и независимая с 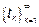
4) Флуктуационный процесс является суммой импульсов.
Исходя из предположений, моделью флуктуационного процесса будет:
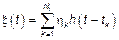
| 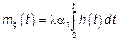 , , 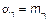
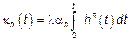 , где , где 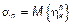 – начальные моменты амплитуды. – начальные моменты амплитуды.
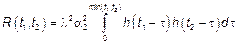
|
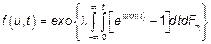
Если 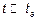 тогда
тогда 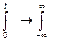 тогда
тогда  – стационарный в узком смысле процесс.
– стационарный в узком смысле процесс.
1. Данная модель пригодна только для стационарных флуктуационных сигналов.
2. Случайными являются только амплитуды.
3. Форма импульса одинакова для всех 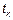
Если 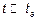
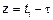

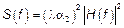
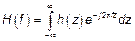
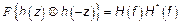
Простейшая модель БШ
 перешли к модели Бунимовича-Райса
перешли к модели Бунимовича-Райса 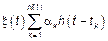
Ограничения 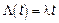 ,
,  (1)
(1)
В результате линейных преобразований часть 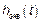 имеет вид,
имеет вид,
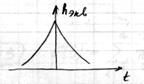
| Поскольку условие (1) не выполняется, то нельзя использовать данные модели.
Второе ограничение :
1) форма импульсов быть различной в разные моменты времени 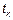 .
2) форма импульсов может зависеть не только от .
2) форма импульсов может зависеть не только от 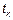 , но и от различных случайных параметров. , но и от различных случайных параметров.
|
Сформулируем основные предположения, необходимые для перехода к модели ПИП.
1) 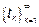 – пуассоновский поток событий, в общем случае – неоднородный, но
– пуассоновский поток событий, в общем случае – неоднородный, но 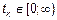 .
.
2) В момент 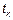 возникают элементарные импульсы, форма которых описывается детерминированной функцией
возникают элементарные импульсы, форма которых описывается детерминированной функцией  , где
, где 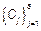 – набор параметров (оговорим, что при
– набор параметров (оговорим, что при 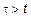 нету )
нету )
3) Постоянные 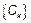 могут быть случайными то есть
могут быть случайными то есть 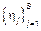 , для удобства
, для удобства 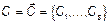
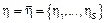
4) 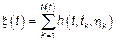 – модель Пуассоновских импульсных процессов.
– модель Пуассоновских импульсных процессов.
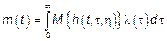 ,
, 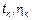 – имеет одинаковый закон распределения.
– имеет одинаковый закон распределения.

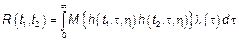
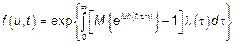
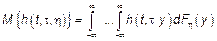 ,
, 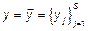 – возможные значения
– возможные значения  .
.
Необходимо вычислить 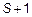 интеграл для
интеграл для 
Принимается  и
и  – независимые СВ, только тогда используют данную модель.
– независимые СВ, только тогда используют данную модель.
Предположим, что
1. в момент времени 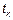 возникают элементарные импульсы,
возникают элементарные импульсы, 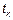 образуют пуассоновскую последовательность на интервале
образуют пуассоновскую последовательность на интервале 
2. форма импульсов описывается детерминированной функцией  , то есть форма импульса может зависеть от
, то есть форма импульса может зависеть от 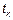 .
.
3. амплитуды импульсов 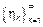 – независимы, одинаково распределенные СВ,
– независимы, одинаково распределенные СВ,  и
и 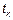 – независимы.
– независимы.
 4. в момент времени
4. в момент времени 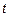 флуктуационный процесс представляет собой сумму элементарных импульсов, то есть
флуктуационный процесс представляет собой сумму элементарных импульсов, то есть 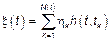 .
.
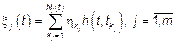 – области
– области 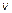 .
.
 , где
, где  – независимая.
– независимая.
Возникает вопрос, связанный с приведением данной модели к компактному виду.
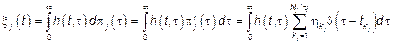 .
.
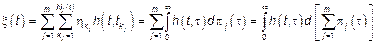
Конечная сумма сложных процессов Пуассона является процессом с независимыми приращениями 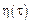 , тогда
, тогда  – ЛСП, где
– ЛСП, где 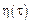 – порождающий процесс,
– порождающий процесс,  – ядро ЛСП.
– ядро ЛСП.

ЛСП – результат фильтрации БШ в узком смысле линейной системой с импульсной характеристикой  .
.
Выводы:
1. ЛСП является суммой большого числа импульсов, форма которых описана  , а параметры импульсов заложены в процессе
, а параметры импульсов заложены в процессе 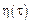 .
.
2. ЛСП – отклик ЛС при воздействии на нее БШ.
Частные случаи модели ЛСП
1. Пусть 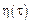 – однородный СП и
– однородный СП и 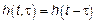 . ЛСП может быть записан в следующем виде
. ЛСП может быть записан в следующем виде 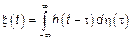 – стационарный в узком смысле СП. БШ в УС –> непараметрическая система –> ЛСП в УС.
– стационарный в узком смысле СП. БШ в УС –> непараметрическая система –> ЛСП в УС.
2. 
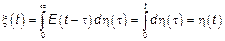 – процесс с независимыми приращениями.
– процесс с независимыми приращениями.
3. 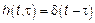 , тогда
, тогда 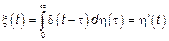 .
.
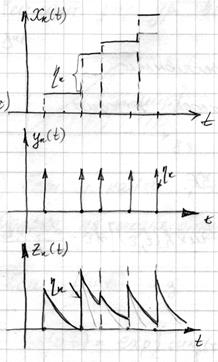
4. 
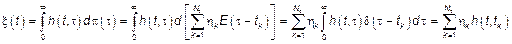 .
.
В качестве модели будем рассматривать ЛСП с однородным 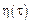 .
.
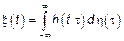
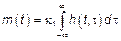
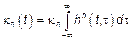 – для линейного СП.
– для линейного СП.

Если 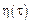 – однородный процесс Пуассона –>
– однородный процесс Пуассона –> 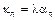 .
.
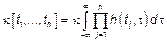
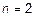
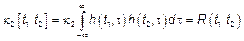 .
.
Для стационарного процесса
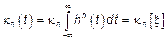

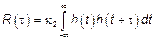
Для ЛСП нахождение 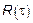
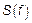 является не эффективным. Для более детального изучения флуктуационных процессов целесообразно находить моменты порядка
является не эффективным. Для более детального изучения флуктуационных процессов целесообразно находить моменты порядка 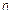 .
.
Наиболее полную характеристику ФП дают их ЗР.
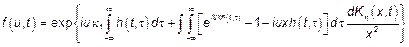
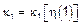
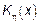 – ПСФ порождающего процесса.
– ПСФ порождающего процесса.
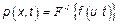
В ряде случаев 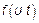 раскладывается в ряд. При условии
раскладывается в ряд. При условии 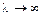 тогда
тогда 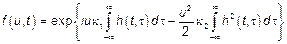 – гауссовская ХФ.
– гауссовская ХФ.
Возникает вопрос – как точно найти ЗР флуктуационного сигнала.
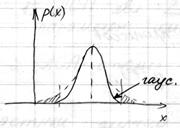
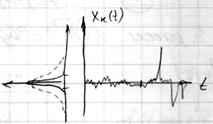
Варианты решения поставленной задачи:
1. Находят 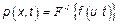 – задача сточки зрения математики не имеет решения в общем случае потому, что ХФ – безгранично делима (БД) (в явном виде вычислить
– задача сточки зрения математики не имеет решения в общем случае потому, что ХФ – безгранично делима (БД) (в явном виде вычислить 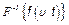 нельзя для БД ).
нельзя для БД ).
 2.
2. 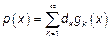 ,
, 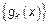 – система ортогональных функций.
– система ортогональных функций.
Это точное представление, но для нахождения 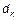 необходимо вычислить
необходимо вычислить  ,
, 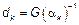 – достоинство данного решения.
– достоинство данного решения.
1) Ограниченность количества слагаемых – недостаток.
2) 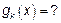 какие брать слагаемые.
какие брать слагаемые.
3.  Решение этого уравнения определяет целую группу распределений – система распределений Пуассона (порядка 13 распределений).
Решение этого уравнения определяет целую группу распределений – система распределений Пуассона (порядка 13 распределений).
Решение дифференциального уравнения выражается через 
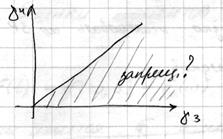
4. Если можно найти 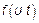 , то надо ее и исследовать. Однако на сегодня отсутствует прикладная теория
, то надо ее и исследовать. Однако на сегодня отсутствует прикладная теория 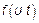 .
.
5. Если 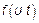 – б.з. –>
– б.з. –> 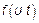 может быть записана в каноническом виде, то есть
может быть записана в каноническом виде, то есть 
Различия двух сигналов будет заключатся в различии параметров
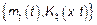
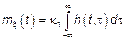
ПСФ  , где
, где 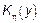 – ПСФ порождает СП
– ПСФ порождает СП 
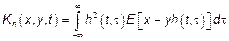
Проблемы могут возникнуть при нахождении пределов интегрирования в явном виде.
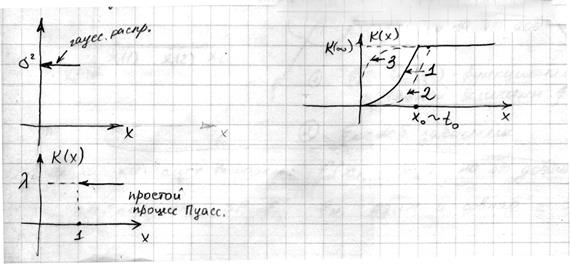
ВЫВОДЫ:
1. Модель линейных СП является наиболее полной моделью флуктуационных сигналов.
2. Имеются формулы для вычисления вероятностных характеристик СП.
3. Для исследования флуктуационных процессов целесообразно исследовать их ЗР или кумулянтные функции высших порядков.
Дата добавления: 2015-08-04; просмотров: 736;
