СП с непрерывными спектрами
1. Спектральное представление СП
2. Спектральная плотность
3. Взаимная спектральная плотность (ВСП)
4. Узкополосный и широкополосный СП
5. Спектральные характеристики линейных преобразований
Если есть СП  тогда
тогда 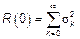 ,
, 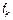 – физический спектр
– физический спектр
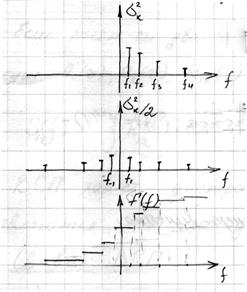 Получили аналогично с прямоугольником распределения
Получили аналогично с прямоугольником распределения

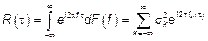
Функция  по своим свойствам ФР , тогда
по своим свойствам ФР , тогда 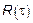 схожа с ХФ.
схожа с ХФ.
Функция  может быть любой, тогда Хинчи исследовал функцию
может быть любой, тогда Хинчи исследовал функцию 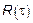 и установил, что если есть ССП
и установил, что если есть ССП  с
с 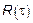 тогда
тогда
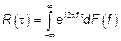 .
.
Свойства  :
:
1) непрерывна слева
2) неубывает
3) 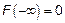 ,
, 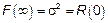
Тогда 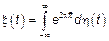 ,
, 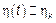 – процесс с ортогональными приращениями
– процесс с ортогональными приращениями
То есть
1) 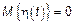
2) Некоррелированние приращения то есть 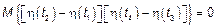
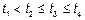
3) 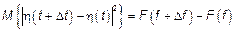
Тогда 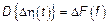
Функция  носит название спектральная функция СП
носит название спектральная функция СП 
ДОПИСАТЬ
Если 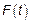 – спектральная функция, то спектр процесса – это множество точек роста спектральной функции(сигнала с конечным спектром).
– спектральная функция, то спектр процесса – это множество точек роста спектральной функции(сигнала с конечным спектром).
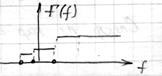
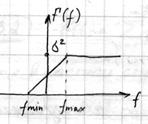
Пусть имеется СП  и имеется
и имеется 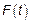 тогда
тогда 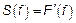 – спектральная плотность
– спектральная плотность
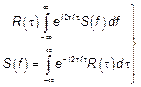 теорема Винера-Хинчича
теорема Винера-Хинчича
А само представление СП сохраняется, то есть 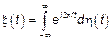
Основные свойства 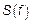 :
:
1) 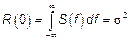
2) 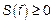 из этого следует, что
из этого следует, что 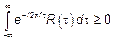 свойство положительной определенности корреляцтонной функция.
свойство положительной определенности корреляцтонной функция.
3) 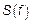 – действительная функция
– действительная функция
4) 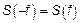
5) 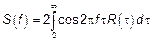
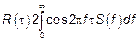
6) 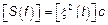 , в частности
, в частности 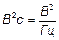
Тогда мы можем установить, что характеризует спектральная плотность.
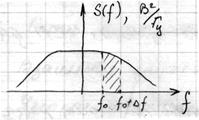
| 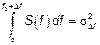 Это дисперсия всех гармонических составляющих процесса
Это дисперсия всех гармонических составляющих процесса  частоты которых принадлежат частоты которых принадлежат 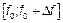 . Спектральная плотность характеризует ту часть дисперсии, которая приходится на полосу . Спектральная плотность характеризует ту часть дисперсии, которая приходится на полосу 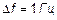 . .
|
Если рассматриваем два СП 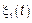 и
и 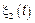 – ССП (стационарно связанные) тогда существует
– ССП (стационарно связанные) тогда существует 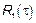 ,
,  ,
, 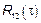
 ,
, 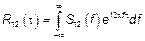
ВСП характеризует дисперсии тех гармонических составляющих, которые являются общими для процессов 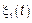 и
и 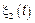 .
.
Свойства ВСП
1) комплекнозначная функция
2) 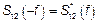
3) 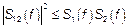
4) 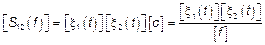
Для двух СП вводится функция когерентности
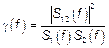
 – схожа с
– схожа с 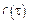 и в частной области характеризует степень линейной связи мезду мгновенными значениями двух СП.
и в частной области характеризует степень линейной связи мезду мгновенными значениями двух СП.
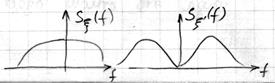
Речь будет идти о ССП  , у которого имеется
, у которого имеется 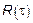 и
и 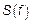 .
.
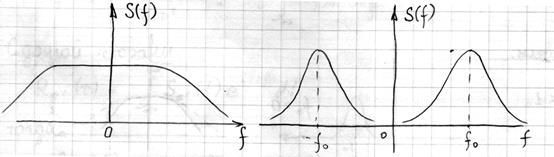
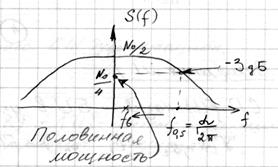
Возникает вопрос: как определить полосу сигнала 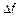 ?
?
1)
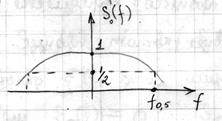
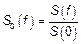 , -3дБ – определение верхней частоты.
, -3дБ – определение верхней частоты.
2) 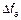

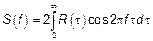
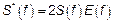

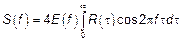
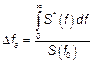
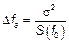
Если низкочастотные процессы, то есть 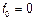 , тогда:
, тогда:
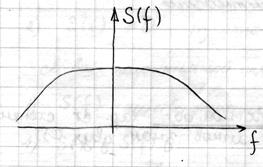
| 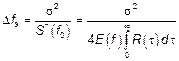 Тогда, пусть
Тогда, пусть
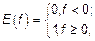
|
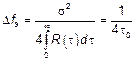 – это справедливо для всех корреляций, которые являются неотрицательными.
– это справедливо для всех корреляций, которые являются неотрицательными.
1) Узкополосные прцессы:
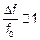
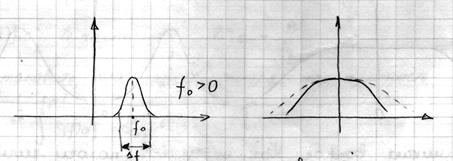
Если 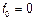 то узкополосность и широкополосность процесса определяется параметрами системы, на которую воздействует этот процесс.
то узкополосность и широкополосность процесса определяется параметрами системы, на которую воздействует этот процесс.
2) Широкополосные процессы.
Пусть 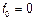
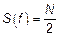 ,
, 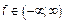 ,
, 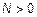 – БШ
– БШ
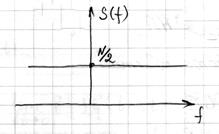
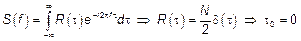
Таким образом – это процесс с некоррелированными мгновенными значениями – БШ в широком смысле.
Самый узкополосный СП – гармоника со случайными параметрами.
5.1. Дифференцирование
Пусть  – СП для которого существует
– СП для которого существует 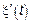 , который также является ССП, то есть
, который также является ССП, то есть 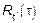 и оба эти СП являются стационарно связанными, то есть
и оба эти СП являются стационарно связанными, то есть  .
.
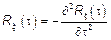 ,
, 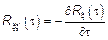
1)
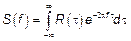
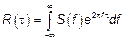
Воспользуемся вторым равенством
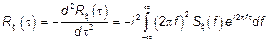
С другой стороны
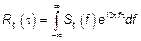
тогда:
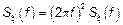

1) Спектр 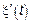 стал шире
стал шире
2) Если 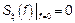
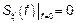 .
.
СП с независимыми приращениями (НП)
1. общие свойства СП с НП
2. Пуассоновский поток событий
3. Пуассоновский СП.
4. Каноническое представление ХФ СП с НП
 называется процессом с независимыми приращениями, если для любых
называется процессом с независимыми приращениями, если для любых 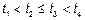 случайные величины
случайные величины 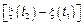 ,
, 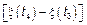 являются независимыми.
являются независимыми.

Запишем процесс  в следующем виде
в следующем виде 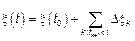 .
.
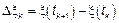
1)Процесс с НП представляет собой суму независимых СВ. Тогда
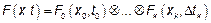 – свертка Стильтьеса.
– свертка Стильтьеса.
Каким образом можно найти ЗР этого СП.
Учитывая сложность нахождения ФР и ПВ используется ХФ, которая будет равна произведению ХФ каждой из величин.
Особенности этих ХФ
Рассмотрим 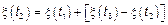
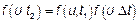
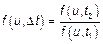
Критерием того, что  – СП с НП является то, что отношение его ХФ в два разных момента времени
– СП с НП является то, что отношение его ХФ в два разных момента времени 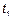 и
и 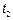 представляет собой ХФ тогда это отношение будет ХФ приращения.
представляет собой ХФ тогда это отношение будет ХФ приращения.
На практике часто 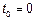 или
или 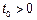 .
.
Эти процессы изучал Поль Леви, он установил, что СП с НП можно представить в следующем виде
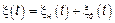
СП называется непрерывным, если 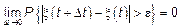
Или можно записать в другом виде:
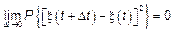
Если у СП 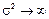 тогда используется первое соотношение.
тогда используется первое соотношение.
Ограничимся СП с НП, у которого дисперсия конечна. Предположим, что 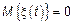 , тогда
, тогда
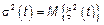
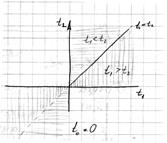
| Введем некую функцию 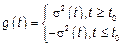 Оказывается, что
Оказывается, что
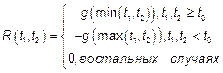 Для того, чтобы СП
Для того, чтобы СП  был непрерывен был непрерывен
|
1) необходимо, чтобы функция 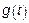 была непрерывна
была непрерывна
2) 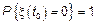 с вероятностью 1 в точке
с вероятностью 1 в точке 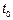 СП равен 0
СП равен 0
У непрерывного СП могут быть разрывы первого рода в некоторых точках 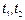 , однако эти точки не являются фиксированными на оси
, однако эти точки не являются фиксированными на оси 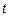 , то есть эти точки образуют случайную последовательность
, то есть эти точки образуют случайную последовательность
СП  является однородным, если любые его распределения приращения
является однородным, если любые его распределения приращения 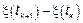 зависят от
зависят от 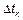 и не зависят от его положения на временной оси, тогда
и не зависят от его положения на временной оси, тогда 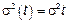 .
.
В дальнейшем будем изучать только 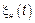 СП с НП
СП с НП
Леви доказал, что любой СП с НП
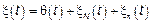
где 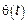 – непрерывная детерминированная функция (неубывающая).
– непрерывная детерминированная функция (неубывающая).
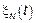 – гауссовский СП с НП.
– гауссовский СП с НП.
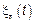 – пуассоновский СП с НП.
– пуассоновский СП с НП.
Для гауссовского СП ХФ имеет вид
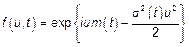
1) 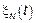 – неоднородное броуновское движение
– неоднородное броуновское движение
2) если 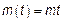 ,
, 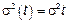 – однородное броуновское движение
– однородное броуновское движение
3) если 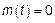 ,
, 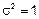 – винеровский СП
– винеровский СП 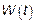 .
.

| 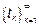 представляет собой точечный СП если представляет собой точечный СП если 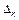 являются случайными величинами с заданными вероятностными характеристиками. являются случайными величинами с заданными вероятностными характеристиками.
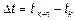
|
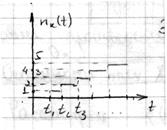 Процесс
Процесс 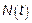 – число точек на
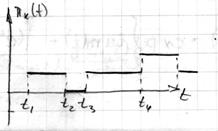
– число точек на 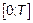 – процесс счета событий. Это целочисленный процесс с реализациями – кусочно-постоянными функциями
– процесс счета событий. Это целочисленный процесс с реализациями – кусочно-постоянными функциями 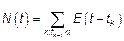
Частные случаи
1) 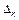 является независимой, одинаково распределенной СВ – процесс восстановления (задачи надежности).
является независимой, одинаково распределенной СВ – процесс восстановления (задачи надежности).
2) 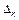 – независимая СВ, распределенная по показательному закону – процесс Пуассона.
– независимая СВ, распределенная по показательному закону – процесс Пуассона.
Обычно процесс Пуассона определяется следующим образом:
Пусть имеется случайная последовательность 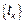 , удовлетворяющая условиям:
, удовлетворяющая условиям:
1) число событий 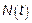 , которые произошли на непересекающихся интервалах времени
, которые произошли на непересекающихся интервалах времени 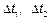 , то есть
, то есть 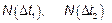 являются независимыми СВ.
являются независимыми СВ.
2) вероятность того, что на промежутке 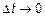 произойдет более одного события равна 0, то есть
произойдет более одного события равна 0, то есть 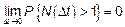 .
.
3) число событий  , которые произошли на интервале
, которые произошли на интервале 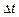 зависит только от длинны этого интервала и не зависит от его положения на временной оси (однородный СП с НП).
зависит только от длинны этого интервала и не зависит от его положения на временной оси (однородный СП с НП).
Этих трех условий достаточно, чтобы получить:
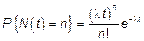 ,
, 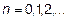 ,
, 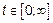
Это распределение Пуассона с параметрам 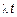 .
.
Тогда автоматически следует, что
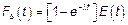
В этом случае последовательность 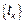 называется пуассоновским потоком событий, тогда
называется пуассоновским потоком событий, тогда 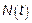 представляет собой однородный СП с НП.
представляет собой однородный СП с НП.
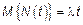 ,
, 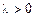 ,
, 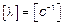 .
.
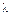 – среднее число событий за единицу времени.
– среднее число событий за единицу времени.
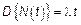 – непрерывная.
– непрерывная.
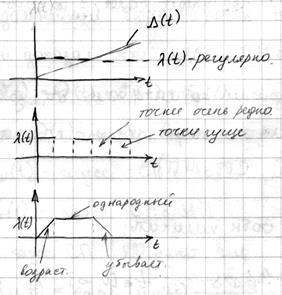
При условии 3) процесс 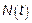 является однородным.
является однородным.
Если убрать это предположение, то в этом случае
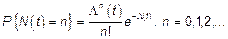
Условия :
1) 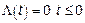
2) 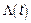 – неубывающая функция.
– неубывающая функция.
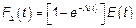
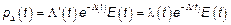 , где
, где 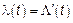 – интенсивность пуассоновского потока событий,
– интенсивность пуассоновского потока событий, 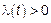 так как
так как 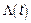 – неубывающая функция.
– неубывающая функция.
Если 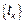 – пуассоновский поток событий, то процесс
– пуассоновский поток событий, то процесс 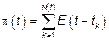 – процесс Пуассона.
– процесс Пуассона.
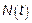 :
: 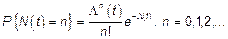
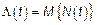
Реализации процесса Пуассона имеет вид
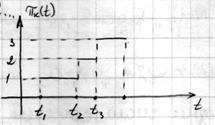
Для того, чтобы процесс был непрерывен необходимо
1) 
2) 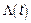 – неубывающая
– неубывающая
3) непрерывна 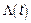
Данный процесс – процесс с непрерывными приращениями, в общем случае неоднородный и стахостически непрерывен.
Основные характеристики Пуссоновского СП
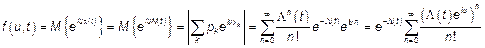
Тогда 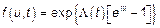
Кумулянты из последней формулы будут иметь вид
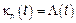 – одномерные
– одномерные
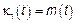 ,
, 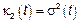
Корреляционная функция. Рассмотрим 
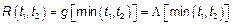
Если 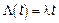 – пуассоновский СП является однородным.
– пуассоновский СП является однородным.
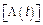 – безразмерная функция, среднее число событий, которые произошли за промежуток времени
– безразмерная функция, среднее число событий, которые произошли за промежуток времени 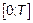 .
.
Формула для 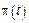 будет одинакова как для однородных, так и для неоднородных СП.
будет одинакова как для однородных, так и для неоднородных СП.
Такого типа процесс – простой процесс Пуассона.
Рассмотрим сложный процесс Пуассона.
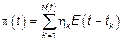 , где
, где 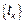 – пуассоновский СП.
– пуассоновский СП.
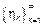 – независимая, одинаково распределенная СВ с ФР
– независимая, одинаково распределенная СВ с ФР 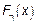 или ХФ
или ХФ 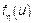
1) Пусть 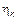 : вырожденная СВ, то есть
: вырожденная СВ, то есть 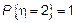
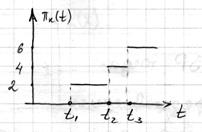
2) 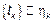 :
: 
в данном примере 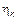 будут иметь разные ЗР
будут иметь разные ЗР
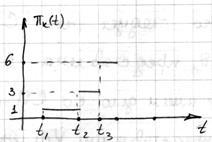
3) 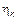 :
: 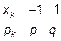
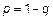
4) Пусть 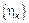 – имеет показательный ЗР
– имеет показательный ЗР
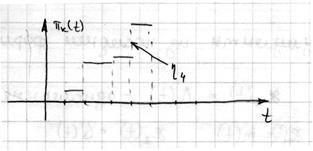
Что можно сказать о мгновенных значениях – они непрерывны.
Если 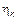 – дискретная СВ –
– дискретная СВ – 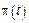 – дискретный СП
– дискретный СП
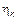 – непрерывная СВ –
– непрерывная СВ – 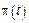 – СП с непрерывными мгновенными значениями.
– СП с непрерывными мгновенными значениями.
ХФ для сложного процесса Пуассона равна:
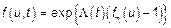
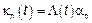 , где
, где 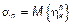
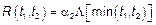
Условие однородности сложного процесса Пуассона – 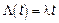
Процесс с независимыми приращениями определяется как
1) 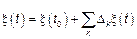
2) 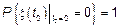 таким образом
таким образом 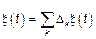
3) 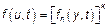 ,
,
Где 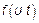 – ХФ приращений.
– ХФ приращений.
Из этого следует, что СП с НП и БДЗР тогда ХФ может быть представлена в трех канонических представлениях.
Так как мы имеем дело со СП с конечной энергией, запишем ХФ в каноническом представлении Калмогорова:
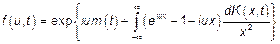
Рассмотрим ХФ пуассоновского сложного процесса
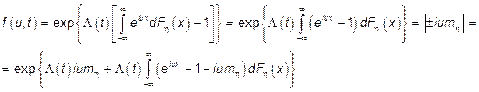
Получаем
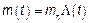
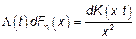
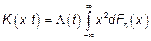
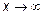
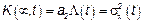
Предположим
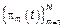 ,
, 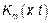
Если 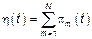 следовательно
следовательно 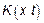 СП
СП  имеет вид
имеет вид
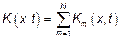 – Пуассоновская спектральная функция сложных пуассоновских процессов.
– Пуассоновская спектральная функция сложных пуассоновских процессов.
Если
1) 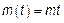
2) 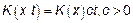
Тогда СП с НП называют однородным СП с НП.
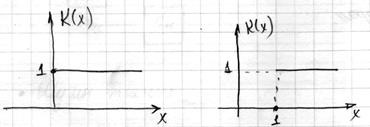
На основании выше сказанного
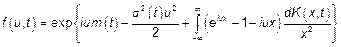
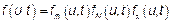
Что соответствует
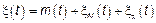
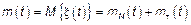
Если у СП с НП 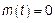 и
и 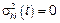 то СП состоит только из пуассоновской составляющей – конечная или счетная сумма независимых сложных пуассоновских процессов.
то СП состоит только из пуассоновской составляющей – конечная или счетная сумма независимых сложных пуассоновских процессов.
Белый шум (БШ)
1. Флуктуационные процессы
2. БШ в широком смысле
3. Связь БШ с процессами с некоррелированными приращениями
4. БШ в узком смысле
Флуктуация – это отклонение микроскопических значений от среднего.
Флуктуационные процессы
1.1 Шумы в электрических приборах
– тепловые
–дробовой шум
–фликкер-шумы
Тепловые шумы
 Тепловой шум пропорционален
Тепловой шум пропорционален 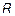 и
и 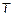 (температура в К). На пассивных элементах (
(температура в К). На пассивных элементах ( 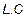 ) шумов нет.
) шумов нет.
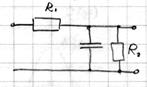
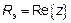

Дробовой шум
Диод, работающий в режиме насыщения: на катоде создается ток электронов, которые при соударении с анодом создают дробовой шум.
Если у нас режим не насыщения, вокруг анода создается пространственный заряд и на анод поступает случайное количество электронов – фликкер-шум.
Все рассмотренные шумы представляют собой последовательность случайных импульсов, возникающих в различные моменты времени.
1.2 Акустические шумы в механических системах.
– акустическая эмиссия


–кавитация
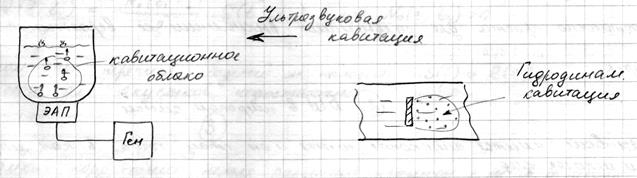
–шумы трения
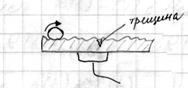
–вибродиагностика
1.3 Биомедицинские сигналы
– шумы дыхания
–шумы сердца
–шумы суставов
–сигналы с мозга – энцифалограмы
Выводы:
– ФП представляет собой результат суммирования бесконечного числа импульсов со случайными параметрами.
–В большинстве случаев спектральная плотность ФП является практически равной в широком диапазоне частот.
–ФП имеют нестационарные характеристики (во многих случаях).
–ЗР ФП отличается от гауссового.
–ФП содержит полезную информацию об исследуемом объекте (техническом или физическом).
Для извлечения полезной информации из этих сигналов необходимо решить две задачи:
1. Выбрать или найти математическую модель.
2. Найти на основе модели вероятностные характеристики.
Модель должна наиболее полно отражать физические процессы в объекте и быть достаточно простой для дальнейших вычислений ее вероятностных характеристик.
2.1. Если имеется сигнал и он стационарен, тогда в качестве модели мы используем следующую:
 ,
, 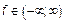 ,
, 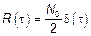
Однако сложно реализовать 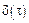 .
.
2.2. Полосовой шум
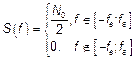
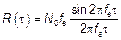
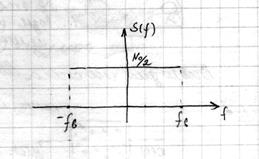
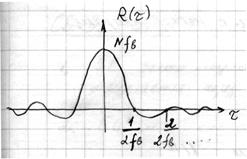
Если 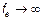 то
то 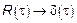
Равномерность спектральной плотности довольно трудно реализовать.
2.3. Розовый шум.
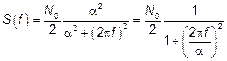
Для того, чтобы считать это БШ необходимо 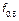 перенести ниже.
перенести ниже.

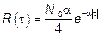
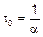
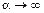
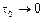 и
и 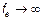
Эти все модели – модели СБШ в широком смысле.
Поскольку БШ – процесс с некоррелированными мгновенными значениями, то можно записать общую формулу, определяющую БШ в широком смысле
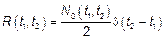 , где
, где 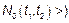
С помощью перечисленных моделей можно находить 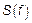 и
и 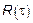 , но этого для акустиков недостаточно.
, но этого для акустиков недостаточно.
В рамках корреляционной теории нельзя различать процессы с независимыми и некоррелированными приращениями.
Пусть  – СП с некоррелированными приращениями
– СП с некоррелированными приращениями 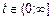 , тогда для него
, тогда для него 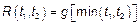 , где
, где 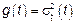 , Оговорка: процесс
, Оговорка: процесс  – стохастически непрерывен
– стохастически непрерывен
Введем процесс 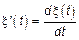 , тогда
, тогда 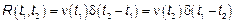
БШ представляет собой производную от процесса с некоррелированными приращениями
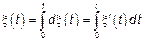 .
.
Определение 1
СП  называется БШ в узком смысле если
называется БШ в узком смысле если 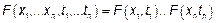 – то есть БШ – процесс с независимыми мгновенными значениями.
– то есть БШ – процесс с независимыми мгновенными значениями.
Определение 2
БШ в узком смысле – это производная от процесса с независимыми приращениями
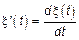
 4.1. Простой процесс Пуассона
4.1. Простой процесс Пуассона
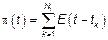
так как БШ это производная от СП с НП получим
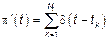
 4.2. Сложный процесс Пуассона
4.2. Сложный процесс Пуассона
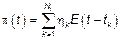
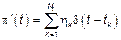
4.3. 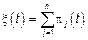 – любой процесс с НП может быть представлен
– любой процесс с НП может быть представлен
суммой сложных процессов Пуассона.
БШ в узком смысле – поток 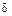 -импульсов со случайными амплитудами, которые возникают в момент времени
-импульсов со случайными амплитудами, которые возникают в момент времени 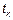 , образующие поток событий
, образующие поток событий 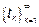
Свойства БШ
1. ЗР БШ определяется через ЗР СП с НП.
2. БШ может быть как стационарен так и не стационарен.
Если 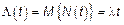 – то пуассоновский БШ будет стационарен.
– то пуассоновский БШ будет стационарен.
3. БШ может быть периодическим и непериодическим.
Если 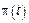 – неоднородный Пуассоновский процесс
– неоднородный Пуассоновский процесс 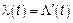 – интенсивность – непериодический.
– интенсивность – непериодический.
Если 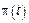 –
– 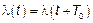 ,
, 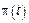 – периодический с периодом
– периодический с периодом 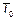 .
.
Дата добавления: 2015-08-04; просмотров: 861;
