Нелинейные преобразования СП

1. Постановка задачи и особенности ее решения.

2. Функция распределения (ФР) отклика нелинейной системы (НС).

3. Двумерная моментная функция отклика НС.

4. Прямой метод нахождения двумерного момента отклика НС.

Если система инерционна (система с памятью), то решить задачу нельзя.

Ограничимся безинерционным классом систем.

,

– динамическая характеристика системы.

Безинерционность системы означает, что .

Если речь идет о СП

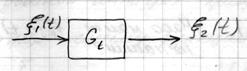
1) Одномерные характеристики – задача решается.

2) Двумерные характеристики – более или менее, моментные функции – какие то решения есть.

Какие характеристики воздействия надо знать, чтобы получить необходимые характеристики отклика?

Если есть СП с ФР , есть функциональное преобразование .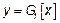

, необходимо найти ФР отклика, то есть

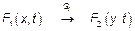
Общий ход решения задачи.

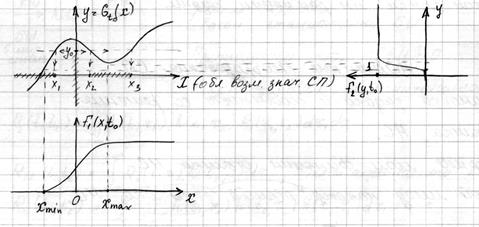
Фиксируем точку 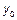. Нас интересует , – преобразование функции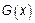

Задача решается в явном виде если 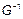является обратной функцией ( – монотонная функция).

3.1. Одномерная моментная функция

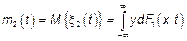надо найти 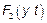, а если не нашли.

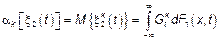
Все центральные моментные функции вычисляются через начальные моментные функции.

3.2. Пусть имеет непрерывные мгновенные значения, то есть существует

Центральные моментные функции выражаются через начальные моментные функции.

Прямой метод основан на разложении двумерной плотности вероятности (ПВ) воздействия в ряды. Наиболее целесообразно использовать ортогональные ряды.

и эта система обладает следующими свойствами

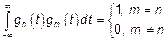Система ортонормированна

Если есть произвольная функция , , тогда может быть представлен в ви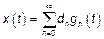де:

, где 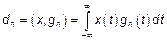– скалярное произведение.

Условия ортогональности можно обобщить вводя так называемые весовые функции.

Для отклика нелинейной системы

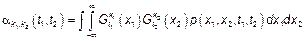
Необходимо двойной интеграл привести к повторному.

Рассмотрим систему функций и эта система удовлетворяет

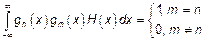
Ортонормированная система с весом

Если – интегрируемость квадрата на бесконечности, тогда

,

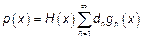Если речь идет о двумерной плотности вероятности

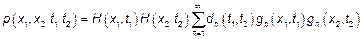
Подставим 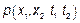в выражение для

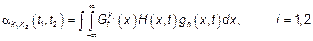
Таким образом

Частный случай, когда 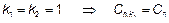получим

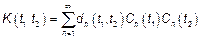
Если удастся разложить двумерную ПВ в ряд, то в задаче нахождения двумерного момента отклика НС сводится к вычислению 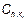. В частности для необходимо вычислить . Результат –выражение в виде ряда.

Трудности: 1) технически трудно вычисл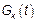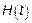ить , , , ;вычислить ; 3) выбор системы ортогональных функций и весовых функций для разложения двумерной ПВ в ряд.