Случайные процессы второго порядка (Марковские процессы)
Исчерпывающей характеристикой случайного процесса является функция распределения
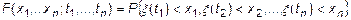
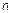 -мерная функция распределения случайного вектора
-мерная функция распределения случайного вектора
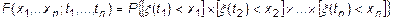
Из курса «ВООД» нам известно, что для произвольных событий 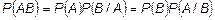 .
.
Для случайных процессов, по аналогии со случайными величинами, функция распределения выражается через условные функции распределения следующим образом
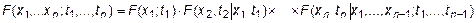
Поясним, что означает запись 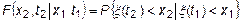
Аналогично можно выразить ПВ и ХФ.
Для независимых СП: СП называется с независимыми мгновенными значениями, если его ФР равна произведению ФР отдельных мгновенных значений, то есть
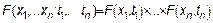 для любого момента времени.
для любого момента времени.
Все условные распределения равны безусловным распределениям.
Для упрощения выражение 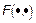 можно ввести индексы соответствующие моментам времени, то есть
можно ввести индексы соответствующие моментам времени, то есть 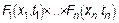 .
.
СП 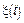 называется процессом с некоррелированными мгновенными значениями, если его корреляционная функция удовлетворяет условию:
называется процессом с некоррелированными мгновенными значениями, если его корреляционная функция удовлетворяет условию:
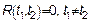 (1)
(1)
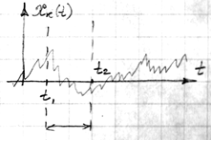
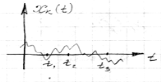
| Возникает вопрос: А что будет если 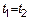 .
Пусть .
Пусть 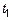 – фиксированная, а – фиксированная, а 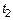 – перемещается.
Если – перемещается.
Если 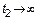 , все ясно.
А если , все ясно.
А если 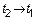 , 1) , 1) 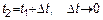
|
Так как СП имеет резко изменяющиеся мгновенные значения, следовательно 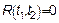 , такие процессы в математике называют "чисто случайными процессами" – физически нереализуемы.
, такие процессы в математике называют "чисто случайными процессами" – физически нереализуемы.
Процесс с независимыми мгновенными значениями называется белый шум в узком смысле.
СП с некоррелированными мгновенными значениями – БШ в широком смысле.
Но в частном случае эти СП можно реализовать эти процессы – когда СП является процессом с дискретным временем.
БШ можно различать по законам распределения(по аналогии со СВ). БШ может быть стационарен и нестационарен.
Часто, вместо выражения (1) имеем следующее выражение:
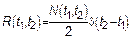 ,
,
где 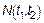 –интенсивность БШ,
–интенсивность БШ, 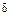 – дельта-функция, в момент времени
– дельта-функция, в момент времени 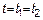 имеем
имеем 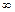 дисперсию.
дисперсию.
Для задания БШ можно описать одномерной ФР потому их называют СП первого порядка.
СП 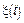 называется Марковским если его ФР удовлетворяет условию
называется Марковским если его ФР удовлетворяет условию
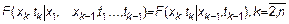
Мгновенные значения СП в момент времени 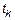 зависят только от мгновенных значений СП в предыдущий момент времени
зависят только от мгновенных значений СП в предыдущий момент времени 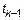 .
.
Часто такие СП называют процессами без последействия.
| Для таких процессов ФР имеет вид:
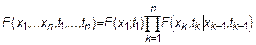
|
Таким образом Марковские процессы можно задать двумя ВР, следовательно их называют СП второго порядка.
СП 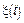 называется процессом с независимыми приращениями если для любого момента времени
называется процессом с независимыми приращениями если для любого момента времени 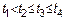 случайные величины
случайные величины 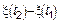 ;
; 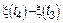 являются независимыми.
являются независимыми.
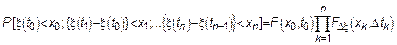 (2)
(2)
Как с помощью выражения (2) можно записать ФР СП 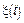 ?
?
СП можно представить в следующем виде:
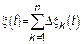
Если СП представляет собой сумму независимых СВ чему б. равна ФР. ФР 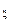 равна свертке ФР приращений.
равна свертке ФР приращений.
В этом случае необходимо использовать ХФ, и в этом случае мы от сверток переходим к произведению. Для СП с НП обычно применяется следующее условие
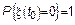 (Все реализации проходят через 0).
(Все реализации проходят через 0).
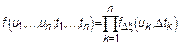
Сколько моментов времени необходимо знать, чтобы задать СП с НП – СП второго порядка.
Данные СП являются подмножеством Марковских СП. Для акустических задач интерес представляют не все МП, с СП с НП.
СП 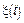 является процесс независимых приращений с некоррелированными приращениями, если для любых моментов времени
является процесс независимых приращений с некоррелированными приращениями, если для любых моментов времени 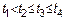 СВ
СВ 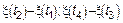 – некоррелированные.
– некоррелированные.
Частный случай: Если СП 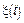 имеет
имеет 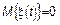 – процесс с ортогональными приращениями.
– процесс с ортогональными приращениями.
СП с некоррелированными приращениями может быть
а) стационарен
б) переодический
Аналитические свойства случайных процессов (СП)
1. Простейшие преобразования СП
2. Непрерывность СП
3. Дифференцирование СП
4. Интегрирование СП
Дата добавления: 2015-08-04; просмотров: 1416;
