ТЕХНОЛОГИЧЕСКИЕ ОСНОВЫ УПРАВЛЕНИЯ ДИСКРЕТНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ

Дискретные производственные процессы характеризуются от­дельными операциями с четко выраженными началом и концом, перерывами с остановкой и выключением технологического обору­дования, относительной универсальностью технологического обо-

рудования, наличием партий при обработке деталей и межопера­ционных заделов (производство мебели, стройдеталей, фанеры и т. д.).

Общий дискретный процесс подразделяют на обрабатывающие и сборочные процессы. Обрабатывающие процессы вы­полняются в цехах предприятия, где выпускают всю номенклатуру деталей, которая с поставками по кооперации обеспечивает работу сборочных цехов.

Конечная цель управления дискретными производственными процессами — обеспечение ритмичной работы, что является одной из наиболее важных и сложных задач.

Для формализации и построения математической модели ди­скретного производственного процесса его разбивают на элемен­тарные операции. Формализованную схему процесса невозможно решить в общем виде. Однако понятие формализованной операции, характеризующей производственный процесс, возможно, если вы­полнение производственной операции над заготовкой или полу­фабрикатом связано с изменением свойств данной заготовки, зна­чения параметров объекта обработки. В этом случае производст­венная операция может рассматриваться как преобразова­тель (оператор), определяющий изменение параметров. Мате­матическая модель производственного дискретного процесса, как совокупность формализованных операций будет представлять собой последовательность операто­ров, перерабатывающих информацию о состояниях изделий (заготовок, полуфабрикатов) в процессе производства. Учитывая принятое деление производственных операций на операции обра­ботки и сборки, будем считать их формализованными, дополняе­мыми при этом формализованной операцией управления. Иногда формализуются и математически описываются некоторые другие операции, присущие конкретному производству.

При построении математической модели (описания) производст­венных операций выбирают систему параметров, описывающих состояние заготовок и других объектов, участвующих в процессе. Каждую операцию выполняют конкретный станок или машина, следовательно, математическое описание устанавливает взаимо­связь параметров станка и заготовки в процессе обработки.

Рассмотрим в качестве примера операции сборки, отличаю­щиеся от операций обработки наличием не менее двух изделий, участвующих в процессе. Моделирование этой операции, которая представляет собой операцию переработки информации о деталях, входящих в сборочный узел, позволяет проанализировать синхро­низацию операций сборки с другими производственными опе­рациями и влияние различных отклонений. Процесс сборки можно представить как присоединение к основной детали l дета­лей.

Наличие деталей обеспечивает течение процесса, и при их от­сутствии операция сборки прерывается. Перед сборкой деталь про­веряют за время 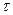_пр. Она может оказаться бракованной с вероят-

ностью Р_6р, тогда ее заменяют новой. Процесс сборки продолжается, пока t_jn < Т, где t_jn — момент поступления очередного ведущего изделия на сборку. Сборка выполняется в определенный отрезок времени, и если процесс не укладывается в норму, происходит срыв операции.

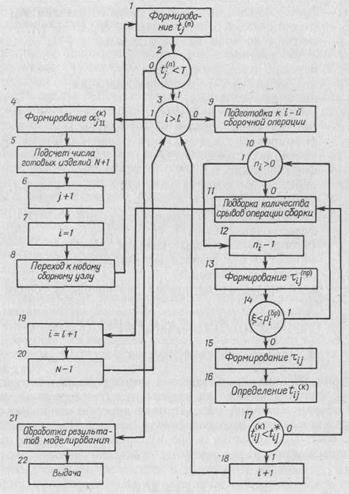
Рис. 97. Блок-схема алгоритма управления операциями сборки

Сборка состоит из совокупности операций 1,2,...,l. Каждая операция соответствует присоединению одной детали n_i к сбороч­ному узлу. Длительность i-й операции для j-го сборочного узла обозначим 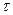_ij, а момент ее окончания 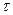_ijk. Если операция не окан­чивается к установленному моменту времени 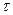_ij то происходит срыв процесса, и j-й сборочный узел исключается из рассмотрения.

Алгоритм, моделирующий формализованную схему операции сборки, будет состоять из следующих операторов [9]:

Ф₁ — формирование момента времени поступления на сборку базовой детали t_jn;

Р₂ — проверка условия t_jn<.T;

Р₃ — проверка условия i>l;

Ф₄ _— формирование параметров готового изделия 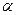_jk;

К₅ — счетчик числа готовых изделий N₁ (N + 1);

К₆— счетчик номеров базовых деталей j + 1;

F₇— формирование i = 1;

F₈ — переход к новому изделию;

F₉— подготовка к i-й сборочной операции;

Р₁₀ — проверка условия n_i>0;

К₁₁— счетчик числа срывов операции сборки;

К₁₂ — счетчик числа деталей номер i (n_i + 1);

Ф₁₃ — формирование длительности проверки детали 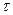_ijпр; Р₁₄ — проверка условия 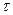<Р_iбр;

Ф₁₅ — формирование 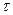_ij;

A₁₆ — определение момента окончания i-й операции t_ijk;

Р₁₇ — проверка условия t_ijk <.t*_ijK;

K₁₈ — счетчик номеров сборочных операций (i + 1);

F₁₉ — формирование i = l + 1;

К₂₀ — счетчик числа готовых изделий (N—1);

A₂₁ — обработка результатов моделирования;

Я₂₂ — выдача результатов.

Схему моделирующего алгоритма для операции сборки можно записать как

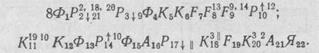
На рис. 97 показана блок-схема моделирующего алгоритма.

В условиях производства встречаются более сложные модифи­кации сборки. Поэтому, рассматривая простую операцию сборки, ее формализованное представление в виде моделирующего алго­ритма, можно подготовить и сформулировать алгоритмы с учетом конкретных условий.