ВЗАИМОСВЯЗЬ ПАРАМЕТРОВ ПРИ МЕХАНИЧЕСКОЙ ОБРАБОТКЕ ДРЕВЕСИНЫ
Деревообрабатывающий станок — это не только комплекс элементов и устройств, рассматриваемых в конструктивном аспекте, но и некоторая технологическая система, где протекают сложные
процессы, характеризуемые рядом физических величин, весомость которых определяется как видом и интенсивностью технологической обработки, так и конструктивными особенностями системы станок— приспособление — инструмент — деталь (СПИД). Все величины, описывающие состояние системы, взаимосвязаны, причем количественные связи могут быть определены физическими закономерностями, которые действуют в реальной системе СПИД, обладающей конечной жесткостью элементов, коэффициентами трения и т. д.
Точность и производительность деревообрабатывающих станков определяют эффективность производства и качество выпускаемой продукции. Поэтому проблема повышения точности и производительности всегда была основной для конструкторов. Современные деревообрабатывающие станки становятся все более сложными и совершенными, оснащенными различными устройствами и системами автоматизации.
Интенсификация работы оборудования — увеличение его производительности—органически связана с увеличением надежности (см. § 44). Процессы механической обработки древесины связаны с энергозатратами, расходом древесного сырья, затратами на инструмент и уход за ним, на оборудование и его обслуживание, на оплату человеческого труда и т. д.
Профессором А. А. Пижуриным [28, 29 ] обосновано, что процессы механической обработки древесины и древесных материалов подвержены влиянию различных факторов, которые можно разделить на следующие группы:
характеризующие объект обработки (породу, влажность, плотность, механические свойства, температуру древесины);
характеризующие инструмент (материал, параметры заточки, степень затупления, величина развода или плющения зубьев, число режущих лезвий, диаметр инструмента или сырья, точность инструмента и др.)
характеризующие процесс механической обработки (размеры стружки, скорости резания и подачи, углы резания, усилия резания и др.);
технико-экономические (себестоимость, производительность обработки и др.).
Математическое описание процессов механической обработки древесины. Это описание состоит в выражении величин yk, характеризующих процесс, в виде функциональной зависимости от различных переменных факторов хi. Зависимости ук = f (xi) для многих процессов механической обработки древесины можно классифицировать как:
1) силовые — по условиям резания Fp = f (хi) и подачи Fn =
= f (хi), по мощностям резания Рр = f (хi) и подачи Рп = f (хi);
2) количественные — по неровностям поверхностей деталей
Рz mах = f (хi); по мощности и ворсистости поверхности W = f (хi);
по точности размерообразований 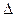 = f (хi); по предельной волни
= f (хi); по предельной волни
стости 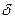 k = f (хi); по поперечной волнистости
k = f (хi); по поперечной волнистости 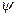 = f (хi);
= f (хi);
3) технико-экономические — по себестоимости обработки с = = f (хi), по производительности обработки П = f (хi).
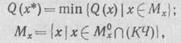
|
| По критерию максимальной производительности: |
Учитывая, что технологические процессы в деревообработке (механическая обработка древесины, гидротермическая обработка древесины, отделка мебели и др.) не поддаются точному теоретическому описанию, построение математических моделей ведут с использованием статистическо-экспериментальных методов. Для этой цели используют теорию планирования эксперимента. Применение активных и пассивных экспериментов позволяет получить зависимость выходной величины от различных воздействий f (хj) в виде уравнений регрессии (см. главу 8). Это особенно эффективно при оценке количественных и качественных показателей технологических процессов деревообработки.
Построение математических моделей занимает значительное место в общем объеме работ по формированию алгоритмов оптимального протекания процессов. Математическая модель должна отражать наиболее существенные черты технологического процесса и позволять последующие исследования на модели и оптимизацию процесса.
Оптимальное протекание процесса определяет целевая функция, которая является критерием оптимизации в пределах заданной области технически допустимых значений технологических параметров. Они определяют область ограничений.
Математические модели и оптимальные задачи [27, 28] могут рассматриваться в нескольких вариантах, основными из которых являются производственный и проектный.
Задачи производственного и проектного вариантов могут решаться по критериям минимальной себестоимости или максимальной производительности.
При решении оптимальных задач производственного варианта математические модели содержат количественные, конструктивно-технологические и технико-экономические ограничения конкретного производственного объекта (участка или оборудования). Во многих случаях ограничениями могут быть производительности соседних участков или необходимость иметь запас по производительности.
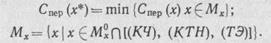
|
| По критерию максимальной производительности: |

|
| В общем виде математические модели [27, 28] механической обработки древесины могут быть выражены целевыми функциями и ограничениями. |
По критерию минимальной себестоимости:
При решении оптимальных задач проектного варианта принимаются соответствующие ограничения, другие ограничения конструктор рассчитывает, исходя из полученных оптимальных режимов
По критерию минимальной себестоимости:

|
где Мх — множество допустимых оптимальных решений; М0х — ограничения, накладываемые множеством и удовлетворяющие технологическим ограничениям вида fi(х) 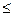 b, i = 1, . . . , т; КЧ, КТН, ТЭ — конструктивно-технологические, качественные и технико-экономические ограничения.
b, i = 1, . . . , т; КЧ, КТН, ТЭ — конструктивно-технологические, качественные и технико-экономические ограничения.
Характеристики ограничений. Количественно ограничения формулируются следующим образом:
1. Конструктивно-технологические ограничения объединяют ограничения по мощности привода главного движения (привода механизма резания).
В общем виде для всех деревообрабатывающих станков потребная мощность резания определяется
Р = KbHu/(60  102) [кВт],
102) [кВт],
где K — удельное сопротивление резания, кГс/мм2, учитывающее вид обработки; b — ширина снимаемого слоя, мм; Н — глубина резания, мм; u — скорость подачи, м/мин.
Ограничение: Рz 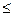 Рн, Рн — номинальная мощность двигателя, кВт.
Рн, Рн — номинальная мощность двигателя, кВт.
Мощность привода подачи
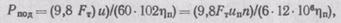
где Ft — тяговое усиление, развиваемое механизмом подачи, Н; 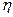 п — КПД механизма подачи
п — КПД механизма подачи
Pпод 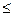 Рн или Ft
Рн или Ft 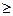
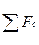 ,
,
где 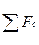 — сумма сил сопротивления подачи, Н, определяемая типом механизма подачи.
— сумма сил сопротивления подачи, Н, определяемая типом механизма подачи.
Зависимость мощностей резания и подачи от параметров процесса раскрывается через усилия резания или подачи.
В группу конструктивных ограничений включают ограничения: по максимальной и минимальной скоростям вращения шпинделя
n 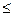 nmax; n
nmax; n 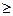 nmin,
nmin,
по наибольшей и максимальной скорости подачи
uz(uz) 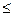 umax(uz max);
umax(uz max);
u(uz) 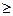 umin(uz min)
umin(uz min)
по глубине резания t 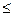 Н (допуск на обработку); t
Н (допуск на обработку); t 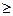 tmin.
tmin.
В зависимости от вида механической обработки древесины могут вводиться дополнительные ограничения, характерные для данного вида обработки. Например, для процесса шлифования вводят ограничения по температуре древесины, при пилении древесины рамными пилами — ограничения по заполнению впадин зубьев, пил, по устойчивости пил и т. д.
Рассматриваемые ограничения выражаются функциональными зависимостями от различных параметров, определяющих режим обработки.
2. Качественные ограничения выражаются в следующем виде: по шероховатости обработки
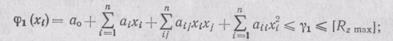 по точности размерообразования
по точности размерообразования
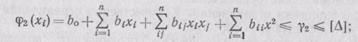 по продольной волнистости
по продольной волнистости
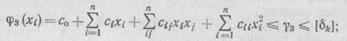 по поперечной волнистости
по поперечной волнистости
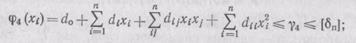 по мшистости и ворсистости
по мшистости и ворсистости
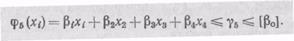 3. Технико-экономическиеограничения, которые при оптимизации процессов в большинстве случаев выступают как целевые функции или критерии оптимальных систем управления
3. Технико-экономическиеограничения, которые при оптимизации процессов в большинстве случаев выступают как целевые функции или критерии оптимальных систем управления
C = f(xi) 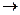 min; П = f(xi)
min; П = f(xi) 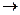 max.
max.
дачи: диапазон, плавность регулирования, стабильность, условия нагрузки и экономичность работы привода.
При вращательном движении узлов станка диапазон регулирования D =  max/
max/  min, где
min, где  mах и
mах и  min — максимальная и минимальная угловые скорости шпинделя, рад/с.
min — максимальная и минимальная угловые скорости шпинделя, рад/с.
У станков с поступательным движением диапазон регулирования определяется требуемым диапазоном линейных скоростей D =
=v max/ v min.
При получении шпона диаметр чурака уменьшается, и для сохранения постоянной скорости резания требуется регулирование скорости привода.
Диапазон регулирования определяется предельными скоростями резания v (м/мин) и предельными диаметрами обработки d (мм)
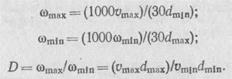
Плавность регулирования определяется отношением двух соседних скоростей  i =
i =  i /
i /  i-1, где
i-1, где  — угловая скорость шпинделя на i-й ступени регулирования, рад/мин.
— угловая скорость шпинделя на i-й ступени регулирования, рад/мин.
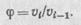
|
| Плавность регулирования ср определяется числом интервалов между скоростями z—1 и диапазоном регулирования D |
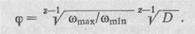
|
Для поступательных движений плавность регулирования
При увеличении числа скоростей в заданном диапазоне регулирования 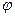
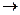 1. Стандартные числа
1. Стандартные числа 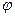 установлены по нормальным рядам чисел в машиностроении и чаще всего применяют значения
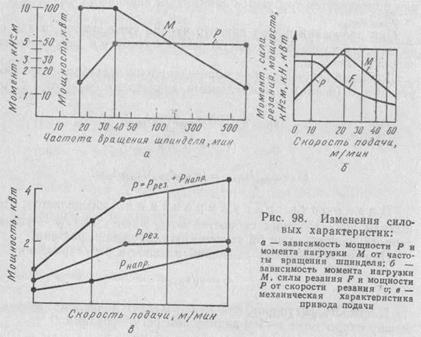
установлены по нормальным рядам чисел в машиностроении и чаще всего применяют значения 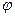 = 1,26; 1,41; 1,58.
= 1,26; 1,41; 1,58.
| § 51. СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕЖИМАМИ ОБРАБОТКИ ДЕТАЛЕЙ Общие понятия.Обработка изделий на деревообрабатывающих станках должна производиться при так называемой экономически выгодной скорости резания, отвечающей наилучшему использованию режущего инструмента и станка. Станок, работая с соответствующими подачей и глубиной резания, должен обеспечивать наибольшую производительность, при высоком качестве обработки. Основные показатели регулирования скорости резания и по- |
Для получения необходимой плавности регулирования, обеспечения требуемого диапазона регулирования и режима резания древесины применяют системы: механического ступенчатого регулирования, электромеханического ступенчатого регулирования и бесступенчатого регулирования.
Приводы станков с главным вращательным движением (кругло-пильные, фрезерные, строгальные и др.), должны иметь постоянную мощность во всем диапазоне изменения частоты вращения шпинделей. Однако использование наибольшей мощности провода при малых частотах вращения привело бы к значительному увеличению габаритов передач, так как в этом случае они должны быть рассчитаны на максимальный момент (Н  м). Мmах= 9554 Pmax/nmin,
м). Мmах= 9554 Pmax/nmin,
где Рmах— максимальная мощность привода, кВт; птiп — минимальная частота вращения, мин-1.
Минимальную частоту вращения выбирают, как правило, не для производительной работы, а для специфических режимов врезания, оцилиндровки и др. Поэтому при малой частоте вращения сохраняется постоянным момент М, допустимый по прочности пе-
редач (Мдоп = const). Следовательно, для станков с главным вращательным движением требуется постоянство мощности в большей части диапазона скоростей и постоянство момента М в нижней части этого диапазона. Графические зависимости мощности Р и момента М от скорости шпинделя для станков с главным вращательным движением представлены на рис. 98, а.
К механическим характеристикам приводов главного движения предъявляют требования высокой жесткости. Продолжительность пуска и торможения главного привода не имеет решающего значения из-за малого влияния на производительность.
К приводам станков с главным прямолинейным возвратно-поступательным движением (фанерострогальные станки) предъявляют требования постоянства момента в большей части диапазона скоростей. При малых скоростях момент М (постоянный) имеет наибольшее значение и, следовательно, сила резания F максимальна. При увеличении скоростей момент М и сила резания F уменьшаются. Трафики зависимости М, F, Р от скорости для станков с главным прямолинейным возвратно-поступательным движением
представлены на рис. 98, б. К приводам этой группы предъявляются требования минимального времени и потерь энергии на реверсирование механизма. Время реверса существенно влияет на производительность и это влияние тем больше, чем меньше длина хода.
Приводы подач станков имеют постоянный момент нагрузки во всем диапазоне регулирования скорости, который обусловливается главным образом моментом трения в направляющих и передачах механизма подачи и может характеризоваться графиком, изображенным на рис. 98, в. В начальной части сохранить постоянство момента не удается вследствие невозможности увеличить глубину резания при малых подачах.
Стабильность работы привода — это изменение скорости при изменении нагрузки, которое зависит от жесткости характеристик двигателя.
За относительное изменение угловой скорости (статизм характеристики) принимается
S=(  o —
o —  н)/
н)/  o =
o = 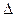
 /
/  o,
o,
где  o и
o и  н — угловые скорости идеального холостого хода и при номинальной нагрузке.
н — угловые скорости идеального холостого хода и при номинальной нагрузке.
Падение скорости при изменении нагрузки от нуля до номинальной для станков устанавливается 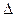

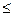 (0,05 ... 0,1)
(0,05 ... 0,1)  во
во
всем диапазоне.
Дата добавления: 2015-07-14; просмотров: 1762;
