По схеме треугольника и звезды

При расчете схемы встречаются сложные соединения, части которых нельзя отнести ни к последовательным, ни к параллельным соединениям. В частности рассмотрим часть схемы в виде треугольника (рис. 22а), вершинами которого А,В,С являются три узла, а сторонами – три резистора R_АВ, R_ВС, R_СА, включенные между этими узлами.

Для упрощения подобных схем во многих случаях бывает удобным заменить треугольник эквивалентной трехлучевой звездой (рис. 22б). Такое преобразование широко применяется при расчетах сложных цепей постоянного тока и цепей трехфазного тока.

Рис. 22

Эквивалентность схем в виде треугольника и звезды получается приравниванием значений сопротивлений или проводимостей между узлами этих схем, отсоединенных от остальной части цепи.

При заданной схеме треугольника (рис. 22а) сопротивления R_А, R_В, R_С эквивалентной звезды (рис. 22б) рассчитываются по формулам:

,

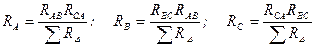где R_АВ, R_ВС, R_СА - сопротивления ветвей треугольника;

∑R_Δ = R_АВ + R_ВС + R_СА - сумма сопротивлений треугольника.

Возможно обратное преобразование звезды из резистивных элементов в эквивалентный треугольник по формулам:

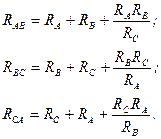
Подробный вывод формул взаимного эквивалентного преобразования треугольника и звезды приведен в [4].

Примером упрощения расчетов может служить преобразование мостовой схемы соединения резистивных элементов (рис. 23а).

После замены одного из треугольников эквивалентной звездой всю цепь (рис. 23б) можно рассматривать как смешанное соединение резистивных элементов.

Рис. 23