В трехфазной схеме, соединенной звездой 2 страница

Следует иметь в виду, что система линейных напряжений на приемнике всегда симметрична вне зависимости от того, есть ли нейтральный провод или он разомкнут. Исключение составляет режим при обрыве линейного провода.

Из равенства (20) можно еще раз убедиться, что при симметричной нагрузке ( 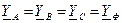) напряжения смещения нейтрали 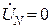(поскольку обращается в ноль числитель, и система фазных напряжений приемника будет симметричной как это следует из равенств (21)).

На рисунке 15 приведена векторная диаграмма фазных напряжений генератора и приемника с несимметричной активной нагрузкой во всех фазах (φ_a = φ_b = φ_c = 0, r_a ¹ r_b ¹ r_c) при обрыве нейтрального провода (U_N > 0).

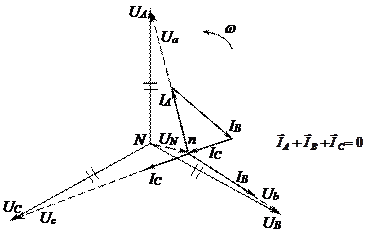
Рис. 15

Из диаграммы видно, что фазные напряжения приемника (они, как и вектор 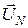, показаны пунктиром) в соответствии с равенствами (21) и (22) представляют собой несимметричную трехлучевую звезду векторов с центром в точке n. Для рассматриваемого случая фазные напряжения U_a > U_A , U_b < U_B , U_c > U_C. Если в качестве активной нагрузки предположить лампы накаливания, то в фазах a–x и c–z приемника лампы будут быстро перегорать, а в фазе b–y гореть вполнакала.

Как видно из диаграммы (рис. 15) токи I_A, I_B, I_C совпадают по фазе со «своими» фазными напряжениями U_a, U_b, U_c и в сумме дают ноль 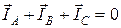в соответствии с первым законом Кирхгофа при обрыве нейтрального провода.

Если восстановить цепь нейтрального провода N–n, то напряжение смещения нейтрали U_N = 0; точка n будет совпадать с нейтральной точкой N генератора, и система фазных напряжений на приемнике станет симметричной.

1.5. Соединение фаз генератора и приемника треугольником

На рисунке 16 показана шестипроводная электрически разобщенная трехфазная схема, подготовленная к соединению генератора и приемника треугольником. Все элементы (напряжения, токи и сопротивления) трех однофазных цепей на этой схеме представлены в виде комплексных чисел.

У трехфазных цепей, соединенных треугольником (условное обозначение D) в отличие от соединения звездой (условное обозначение Y) нейтральный провод отсутствует.

Рис. 16

Чтобы получить соединение фазных обмоток генератора треугольником (рис. 16), подключим конец X первой обмотки к началу B второй обмотки, конец Y второй обмотки – к началу C третьей, конец Z третьей – к началу A первой обмотки. Получается замкнутый сам на себя контур (треугольник), в котором действует симметричная система фазных напряжений 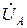, , 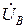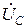. Никакого дополнительного (уравнительного) тока в контуре при этом не возникает, поскольку сумма фазных э.д.с. (напряжений) равна нулю ( 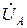+ + 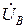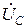= 0), как это было показано раньше (см. раздел 1.1).

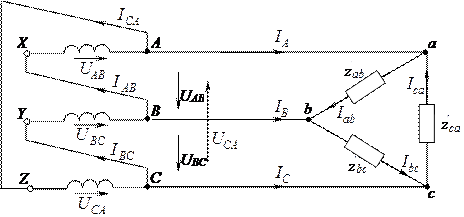
Рис. 17

На рисунке 17 показана электрически связанная трехпроводная схема, в которой генератор и приемник соединены треугольником. После объединения фаз генератора и приемника напряжения между концом и началом каждой фазы не изменятся, то есть эти напряжения одинаковы для несвязанной (рис. 16) и связанной (рис. 17) схем. Поэтому не изменятся и токи в фазах приемника 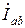, , 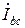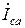в связанной схеме (рис. 17), то есть они будут такими же, как и в несвязанной (рис. 16).

Таким образом из самого принципа соединения в треугольник следует вывод: при соединении треугольником фазное напряжение равно линейному

Это объясняется тем, что потенциал конца предыдущей фазы является также потенциалом начала следующей фазы. Поэтому напряжение между началом и концом фазы (фазное напряжение U_Ф) одновременно является и напряжением между началами двух разных фаз (линейным напряжением U_Л).

Что касается соотношений между линейными и фазными токами, то при замене шести проводов, соединяющих генератор с приемником в несвязанной схеме (рис. 16), тремя линейными проводами A−a, B−b, C−c в связанной схеме (рис. 17), необходимо учитывать наличие электрических узлов A, B, C и a, b, c, в которых распределение токов подчиняется первому закону Кирхгофа [1], [2].

Применив этот закон к соответствующим электрическим узлам приемника или генератора (рис. 17), можно получить следующие соотношения в векторной форме

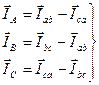
Как следует из равенств (24), вектор линейного тока (его действующего значения) равен геометрической разности векторов соответствующих фазных токов, образующих с этим линейным током электрический узел.

Нетрудно видеть из равенств (24), что сумма линейных токов всегда тождественно равна нулю

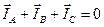В данном случае это векторная сумма. В аналитическом и символическом методах расчета эта сумма алгебраическая (соответственно мгновенных значений и комплексов токов) [1].

Равенство нулю суммы линейных токов любой трехпроводной трехфазной схемы можно объяснить с позиций здравого смысла – методом доказательства от противного. Невыполнение этого равенства означает, что в каждый момент времени от генератора (или приемника) течет большее число зарядов, чем обратно. Это означает, что потенциалы на фазах генератора (или приемника) будут возрастать вплоть до бесконечно большой величины, чего на практике не наблюдается.

Несколько замечаний относительно обозначений физических величин в схеме треугольника. В отличие от соединения звездой для фазных токов и напряжений генератора и приемника, а также для сопротивлений фаз приемника применяется двойная индексация, например, U_AB, I_bc, z_ca, что объясняется равенством линейного и фазного напряжения, то есть каждая фаза оказывается подключенной к двум линейным проводам из трех: А–a, В–b, С–c (рис. 17). Что касается токов в линейных проводах, то они, как и при соединении, звездой индексируются одной большой буквой: I_A, I_B, I_C.

1.6. Режимы работы трехфазной цепи при соединении треугольником

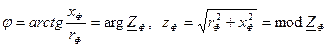Рассмотрим режим симметричной нагрузки. Как и при соединении звездой симметричной называется нагрузка, если комплексные сопротивления фаз приемника равны друг другу, то есть Z_ab = Z_bc = Z_ca = Z_Ф = z_Фe^jφ = r_Ф + jx_Ф, где [1].

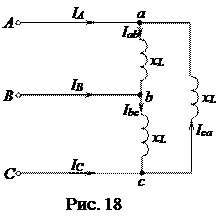
На рисунке 18 показана схема симметричного приемника, соединенного треугольником, в фазы которого включены идеальные катушки индуктивности: Z_ab = Z_bc = Z_ca = Z_Ф =+ jx_L = x_Le^+jπ/2. Поскольку система фазных напряжений на зажимах приемника всегда симметрична, так как она является симметричной системой линейных напряжений генератора, то векторная диаграмма фазных напряжений на рисунке 19 представляет собой симметричную звезду.

Очевидно токи в фазах приемника будут одинаковы по величине 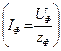и отставать от «своих» фазных напряжений на угол 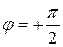, как это показано на рисунке 19. Нетрудно убедиться, что система векторов фазных токов также симметрична.

Для установления количественных связей между фазными и линейными токами на рисунке 20 показано построение векторов линейных токов с использованием симметричной звезды векторов фазных токов без ее увязки с векторами напряжений.

Рис. 20

Сплошными линиями показаны векторы линейных токов 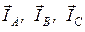, построенных по правилу сложения векторов методом многоугольника (треугольника) в соответствии с записью по первому закону Кирхгофа в виде:

.

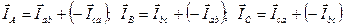Полученная симметричная звезда векторов линейных токов отстает от звезды векторов фазных токов на угол 30°.

Векторная диаграмма линейных токов может быть представлена более компактно в виде сторон правильного (равностороннего) треугольника (рис. 20), вершинами которого являются концы векторов фазных токов (эти векторы показаны пунктирными линиями).

При рассмотрении этого треугольника, сторонами которого являются векторы линейных токов, можно убедиться, что векторная сумма этих токов действительно равна нулю в соответствии с равенством (25).

Очевидно и при несимметричной нагрузке можно также показывать векторы линейных токов в виде векторного треугольника, вершинами которого будут концы векторов фазных токов, представленных в виде несимметричной звезды векторов.

Для определения соотношения линейных и фазных токов при симметричной нагрузке рассмотрим прямоугольный треугольник Dmq0 на рисунке 20. Он получается, если из вершины тупого угла равнобедренного треугольника опустить высоту, которая является и медианой, то есть отрезок 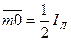(это катет, прилежащий к углу 30°). Гипотенуза рассматриваемого треугольника – отрезок 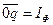. Можно представить отрезок 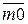как линию косинуса, то есть 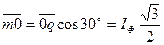. Поскольку , то приравняв правые части последних равенств и сократив на 1/2, получим

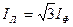Таким образом при симметричной нагрузке (и только при симметричной нагрузке) линейный ток в 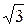больше фазного тока 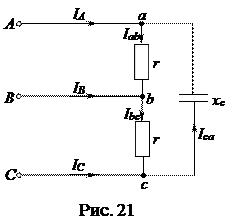( 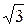= 1,73).

Рассмотрим частный случай несимметричной нагрузки – равномерную нагрузку. На рисунке 21 показана схема приемника, соединенного треугольником, у которого сопротивления фаз, а следовательно, и фазные токи равны друг другу (I_ab = I_bc = I_сa = I_Ф), а углы сдвига φ различны: φ_ab = 0, φ_bc = 0, φ_ca = –π/2.

На рисунке 22 показана векторная диаграмма рассматриваемой цепи. Система фазных напряжений представлена симметричной звездой векторов 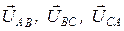. Токи в фазах 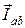и 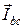совпадают по фазе со «своими» напряжениями и сонаправлены с их векторами (φ_ab = 0, φ_bc = 0). Вектор тока 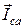опережает вектор напряжения U_CA на угол π/2. Векторы линейных токов 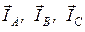показаны пунктиром в виде сторон треугольника, вершинами которого являются концы векторов фазных токов (по аналогии с диаграммой на рисунке 20).

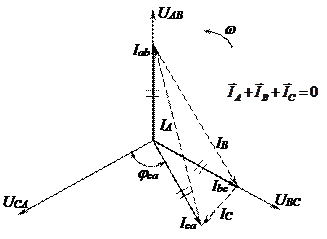
Рис. 22

Как видно из диаграммы на рисунке 22 треугольник векторов линейных токов не является равносторонним, поскольку равномерная нагрузка не является симметричной, хотя фазные токи одинаковы по величине.

Интересно отметить, что в рассматриваемого случае равномерной нагрузки один из линейных токов оказался (рис. 22) меньше фазного: I_C < I_Ф.

Сравним условия работы приемника при соединении его фаз треугольником и звездой.

Схема соединения трех фаз приемника треугольником не зависит от схемы соединения фаз генератора, так как приемник подключается только к трем линейным проводам. Поскольку система линейных напряжений всегда симметрична, а для треугольника они являются фазными, то можно сделать очень важный вывод: при соединении приемника треугольником обеспечивается независимость работы его фаз. Это объясняется тем, что напряжение каждой фазы есть величина постоянная, не зависящая от режима работы других двух фаз, который влияет только на изменение величины токов в линейных проводах.

Ранее было отмечено, что независимость работы фаз несимметричного приемника, соединенного звездой, обеспечивается только при наличии нейтрального провода.

1.7. Мощность трехфазной цепи

Поскольку трехфазная цепь представляет собой совокупность трех однофазных цепей, то мощность трехфазной цепи равна сумме мощностей всех трех фаз.

Как известно [1], в цепях синусоидального тока различают понятия мгновенной, активной (средней за период), реактивной и полной (кажущейся) мощностей.

Напомним выражение для мгновенной мощности [1] однофазной цепи

где P = UIcosφ – активная мощность;

S = UI – полная мощность ,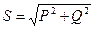

Q = UIsinφ – реактивная мощность;

φ – угол сдвига между током I и напряжением U на входе цепи ; .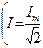

.

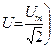Будем рассматривать трехфазную цепь, соединенную звездой с нейтральным проводом, в общем случае несимметричной нагрузки. Запишем выражения для мгновенных мощностей фаз приемника

p_A = u_Ai_A; p_B = u_Bi_B; p_C = u_Ci_C.

При наличии нейтрального провода система фазных напряжений не приемнике симметрична, то есть

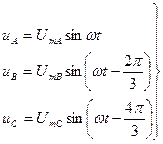
Если приемник несимметричен (Z_a ¹ Z_b ¹ Z_c), то мгновенные значения фазных (линейных) токов можно записать в виде:

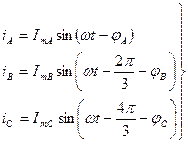
Сделав подстановки (28) и (29) в формулы мгновенных мощностей, получим по аналогии с (27) следующие зависимости:

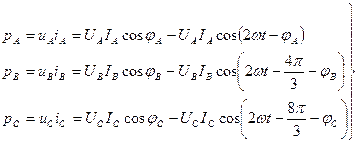
Активная (средняя за период) мощность трехфазной цепи равна сумме активных мощностей всех трех фаз

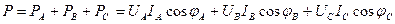
Соответственно реактивная Q и полная S мощности трехфазной цепи равны

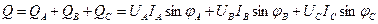
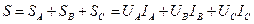
Рассмотрим случай симметричной нагрузки, при которой U_A = U_B = U_C = U_Ф, I_A = I_B = I_C = I_Ф, φ_A = φ_B = φ_C = φ.

Сделав соответствующие подстановки в равенство (31), получим

После аналогичных подстановок в равенства (30) можно получить суммарную мгновенную мощность симметричного приемника в виде

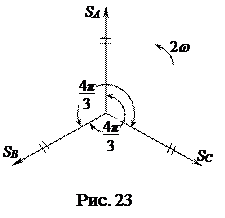
поскольку три косинусоиды двойной частоты 2ω с одинаковой амплитудой U_ФI_Ф = S_Ф при суммировании обращаются в ноль, так как сдвинуты на угол 4π/3относительно друг друга, образуя симметричную звезду векторов (рис. 23).

Таким образом, в отличие от однофазной цепи, мгновенная мощность в которой пульсирует с двойной частотой относительно средней (активной) мощности Р (27), мгновенная мощность трехфазной цепи p при симметричной нагрузке есть величина постоянная p = 3P_Ф = const, то есть не содержит пульсирующих составляющих.

Поэтому трехфазная цепь при симметричной нагрузке называется уравновешенной, в отличие от однофазной цепи, которая является неуравновешенной.

Трехфазные электродвигатели (асинхронные и синхронные), которые являются симметричными приемниками, потребляют из питающей сети мощность и развивают вращающий электромагнитный момент, не содержащие пульсирующих с двойной частотой составляющих (в отличие от двигателей однофазного тока).

Для симметричных приемников, соединенных звездой или треугольником, принято активную, реактивную и полную мощности [1] выражать в расчетных формулах через линейные величины напряжений и токов.

При соединении звездой: .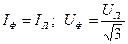

Активная мощность:

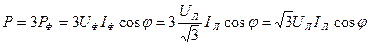Реактивная мощность:

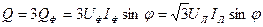Полная (кажущаяся) мощность:

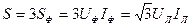При соединении треугольником: .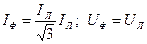

Активная мощность:

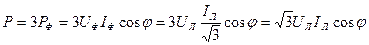
Реактивная мощность:

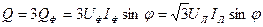
Полная (кажущаяся) мощность:

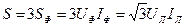
Таким образом расчетные формулы мощности получаются одинаковыми при соединении фаз симметричного приемника и звездой и треугольником.

Необходимо помнить, что угол φ в этих формулах – это угол сдвига между фазными токами и фазными напряжениями.

Сравнение условий работы симметричного приемника при соединении его фаз треугольником и звездой. Соединение фаз приемника треугольником часто переключается на соединение звездой для изменения величины тока и мощности, например, для уменьшения температуры трехфазных электрических печей и т.д.

На рисунке 24 показана схема симметричного приемника, фазы которого a–x, b–y, c–z с помощью переключателя П можно соединить либо звездой (нижнее положение переключателя), либо треугольником (верхнее положение).

Рис. 24

Линейное напряжение питающей трехфазной сети А, В,С обозначим U_Л (на рис. 24 показано U_Л = U_АВ).

Предположим, что при замкнутом трехполюсном рубильнике Р переключатель П находится в нижнем положении (Y), то есть приемник подключен к питающей сети звездой, поскольку концы фаз x, y, z объединены в электрический узел n – нейтральную точку.

Фазное напряжение приемника, соединенного звездой: 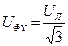. В соответствии с законом Ома фазный (линейный) ток .

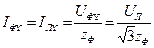Если переключатель П переведен в верхнее положение (D), то приемник оказывается включенным треугольником. При этом фазное напряжение 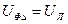; фазный ток 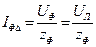; линейный ток 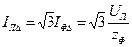. Отношение линейного тока 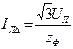треугольника к линейному току 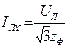звезды:

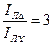то есть при включении приемника треугольником ток в линии в три раза больше, чем при соединении звездой (фазный ток – в 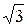раз: ).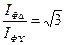

Поскольку формулы мощности симметричного приемника, выраженные через линейные напряжения и токи, одинаковы для звезды и треугольника (36), (37), (38), а линейное напряжение в питающей линии одно и то же U_Л, то в соответствии с (39) справедливы следующие соотношения:

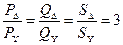Рассмотренная выше (рис. 24) схема переключения симметричного приемника применяется в частности при пуске мощных асинхронных двигателей с короткозамкнутым ротором, у которых в нормальном рабочем режиме обмотка статора должна быть включена треугольником. Прямой пуск таких двигателей (включением обмотки статора непосредственно в питающую сеть) недопустим в виду больших пусковых токов, превышающих номинальный ток в 4¸7 раз. Такие большие токи создают значительные потери («просадки») напряжения в питающей линии, что неблагоприятно сказывается на работе других потребителей, питающихся от этой же сети. Поэтому существует ряд схем пуска мощных двигателей, снижающих пусковые токи (автотрансформаторный пуск, включение в цепь статора токоограничивающих реакторов).

Рассмотренная схема (рис. 24) позволяет снизить ток в питающей линии в три раза. Для этого на период пуска фазы обмотки статора включаются звездой, а после разгона ротора переключаются на треугольник. Недостатком такой схемы пуска является снижение пускового момента, зависящего от квадрата фазного напряжения, в три раза. Поэтому такой пуск обычно применяют при отсутствии нагрузки на валу (вхолостую).

2. Электрические измерения в цепях синусоидального тока

2.1. Общие замечания

При изучении этого раздела необходимо предварительно проработать материал методических указаний для студентов заочной формы обучения «Электроизмерительные приборы», где рассмотрены устройство и принцип действия амперметров, вольтметров, ваттметров и фазометров, применяемых для измерений соответствующих электрических величин в цепях однофазного и трехфазного синусоидального тока. Это в основном стрелочные приборы электромагнитной и электродинамической системы, используемые при выполнении измерений в учебной лаборатории переменного тока кафедры «Электромеханические комплексы и системы» ПГУПСа.

Данная методичка указана в списке литературы настоящего пособия под номером [3].

2.2. Измерения тока и напряжения в цепях синусоидального тока. Расширение пределов измерения

Рассмотрим материал этого раздела применительно к однофазным цепям. Измерения тока и напряжения в цепях синусоидального тока мало чем отличаются от измерений в цепях постоянного тока. Как известно [3], при измерениях в цепях постоянного тока верхний предел измерений амперметров можно увеличить с помощью встроенных или внешних шунтов, а верхний предел вольтметров – с помощью дополнительных резисторов, включаемых последовательно с измерительной цепью вольтметра [3].

В цепях синусоидального тока для этих целей используются измерительные трансформаторы тока и измерительные трансформаторы напряжения [8], [9].

На рисунке 25 показана схема включения амперметра и вольтметра в однофазную цепь синусоидального тока с помощью измерительных трансформаторов. При этом измерительные трансформаторы напряжения применяют в цепях с напряжением выше 1000 В, а трансформаторы тока как в низковольтных, так и высоковольтных цепях (в зависимости от ожидаемой величины измеряемого тока).

Рис. 25

Поскольку измерительные трансформаторы вносят дополнительные погрешности в результаты измерений, то для обеспечения более высокой точности выбирают измерительные трансформаторы с классом точности [3] выше, чем класс самих измерительных приборов.

При включении амперметров и вольтметров через измерительные трансформаторы соответственно тока и напряжения цены деления шкалы определяются с учетом коэффициентов трансформации K_I трансформатора тока и K_U трансформатора напряжения [8].

Измерение токов и напряжений в цепях трехфазного тока практически не отличаются от аналогичных измерений в цепях однофазного тока, в том числе и при использовании измерительных трансформаторов для расширения пределов измерения.

2.3. Измерение мощности и коэффициента мощности