В трехфазной схеме, соединенной звездой 3 страница

в цепях однофазного тока

Когда речь идет об измерении мощности в цепях переменного, в частности синусоидального однофазного тока, то имеется в виду, как правило, активная мощность Р, которую можно непосредственно измерить однофазным ваттметром электродинамической системы [3].

Однако в ряде случаев необходимо также получить с помощью измерений информацию и о величине реактивной Q и полной (кажущейся) S мощности [1]. Очевидно для получения такой информации включения в цепь только одного прибора (ваттметра) недостаточно.

Рассмотрим вначале схему включения ваттметра в однофазную высоковольтную цепь через измерительные трансформаторы напряжения и тока (рис. 26).

Как известно генераторные зажимы вольтметровой и токовой цепей ваттметра обозначаются звездочками (или точками) [3]. При использовании измерительных трансформаторов необходимо следить за правильным включением (рис. 26) начал и концов обмоток трансформаторов и генераторных зажимов обмоток ваттметра (Л₁, Л₂ – зажимы первичной, а и₁, и₂ – зажимы вторичной обмоток трансформатора тока).

Рис. 26

В дальнейшем будем показывать схемы включения измерительных приборов без измерительных трансформаторов, полагая, что в случае необходимости они могут быть предусмотрены в соответствии со схемами на рисунках 25 и 26.

Рассмотрим две схемы включения трех приборов: A, V, W и A, V, φ (рис. 27а и 27б), позволяющие получить информацию о мощностях: активной Р, реактивной Q, полной S, а также о величине коэффициента мощности cosφ.

На рисунке 27а в цепь синусоидального тока с активно-реактивным приемником, комплексное сопротивление которого Z = r + jx = ze^jφ, причем в общем случае реактивное сопротивление x = x_L – x_C [1], включены амперметр А, вольтметр V и ваттметр W.

Рис. 27

Амперметр и вольтметр показывают действующие (средние квадратичные за период Т) значения тока I и напряжения U на входе цепи, а ваттметр показывает активную (среднюю за период) мощность P = UIcosφ [Вт].

Используя показания амперметра и вольтметра, можно получить величину полной (кажущейся) мощности S = UI [ВА]. Из треугольника мощностей [1], используя теорему Пифагора, можно вычислить величину реактивной мощности 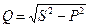[вар]. И наконец, используя показания всех трех приборов, можно определить коэффициент мощности

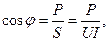
где 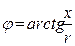– угол сдвига по фазе между током I и напряжением U на входе цепи.

Аналогичную информацию можно получить, заменив в рассмотренной схеме (рис. 27а) ваттметр W на фазометр φ (рис. 27б). Как известно [3], схема включения фазометра электродинамической системы аналогична схеме включения ваттметра. Фазометр показывает угол φ сдвига между током I и напряжением, подаваемом на вольтметровую обмотку прибора (на схеме рисунка 27б – это напряжение U на входе цепи).

По показаниям амперметра А и вольтметра V определяется полная мощность S = UI. На фазометре шкала в градусах угла φ обычно совмещена со шкалой cosφ. Это позволяет непосредственно измерить коэффициент мощности 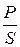[1]. Косвенным путем можно получить величину активной мощности P = UIcosφ и реактивной мощности .

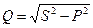Таким образом для получения полной информации о величинах тока, напряжения, активной, реактивной и полной мощности, а также коэффициента мощности cosφ [1], необходимо включить в однофазную цепь три электроизмерительных прибора из четырех (амперметр, вольтметр, ваттметр, фазометр).

На схемах рисунков 27а и 27б использованы амперметр и вольтметр в комбинации либо с ваттметром, либо с фазометром.

Очевидно, возможны и редко применяемые схемы, в которых использованы ваттметр и фазометр в комбинации либо с амперметром, либо с вольтметром. Действительно по показаниям ваттметра и фазометра можно определить полную мощность 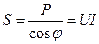. Поэтому достаточно включить дополнительно или амперметр или вольтметр, чтобы измерить соответственно величину напряжения или тока, то есть получить всю недостающую информацию.

2.4. Измерение мощности в трехфазных цепях

Как уже упоминалось, схема включения амперметра и вольтметра для измерений тока и напряжения в трехфазных цепях та же, что и в однофазных цепях. Конкретная схема включения ваттметров для измерения мощности определяется: схемой цепи (трех- или четырехпроводная), способом соединения фаз приемника (звезда или треугольник), характером нагрузки (симметричная или несимметричная).

При несимметричной нагрузке активную мощность измеряют тремя ваттметрами, каждый из которых измеряет мощность одной фазы. Для этого по токовой цепи ваттметра должен протекать фазный ток, а на вольтметровые зажимы прибора должно быть подано фазное напряжение.

Рис. 28

На рисунке 28 показана схема трех ваттметров для измерения активной мощности в «четырехпроводной звезде» при несимметричном приемнике (Z_a ¹ Z_b ¹ Z_c). Эта схема позволяет получить активную мощность в виде суммы показаний трех ваттметров, измерительный механизм каждого из которых перемножает фазное напряжение на «свой» фазный ток и на косинус угла между ними.

Рис. 29

Метод трех ваттметров при соединении фаз несимметричного приемника треугольником (схема включения ваттметров представлена на рисунке 29) применяется редко, поскольку приходится «внедряться» с токовыми обмотками ваттметров в саму схему треугольника. Поэтому предпочтение при соединении приемника треугольником отдается схеме двух ваттметров, о которой пойдет речь в дальнейшем.

Рассмотрим сначала измерения активной мощности симметричного приемника методом одного ваттметра. Является очевидным, что измерив мощность одной фазы, достаточно умножить на три полученную величину или соответствующим образом отградуировать шкалу прибора.

Поскольку при соединении звездой симметричного приемника нейтральный провод отсутствует, то возникают проблемы включения вольтметровой цепи на фазное напряжение (между линейным проводом, по которому течет фазный ток, и нейтральным проводом).

Рис. 30

На рисунке 30 представлена схема включения ваттметра в фазу А симметричного приемника при доступной нейтральной точке n.

Если симметричный приемник соединен треугольником, то схема измерения имеет вид, представленный на рисунке 31. Недостаток этой схемы тот же самый, который обсуждался при рассмотрении метода трех ваттметров (рис. 29) применительно к приемнику, соединенному треугольником.

Рис. 31

У большинства стационарных симметричных приемников имеется только три зажима для присоединения его к трехфазной трехпроводной сети. В этих случаях применяют схему включения ваттметра с искусственной нейтральной точкой (рис. 32).

Искусственную нейтральную точку n₁ создают, включая звездой два резистора с сопротивлением R и параллельную (вольтметровую) цепь ваттметра с сопротивлением R_V, причем R = R_V, то есть получается симметричная звезда резисторов, на которой выделяется необходимое для ваттметра фазное напряжение.

Рис. 32

При соединении приемника звездой I_Л = I_Ф, поэтому ваттметр измеряет активную мощность фазы А (рис. 32). Поскольку соединение треугольником всегда может быть эквивалентно преобразовано в соединение звездой [2], то схема на рисунке 32 может быть применена как при соединении фаз симметричного приемника звездой, так и треугольником. Для получения искомой трехфазной мощности надо умножить показание ваттметра на три или отградуировать соответствующим образом шкалу прибора.

Метод двух ваттметров широко применяется в трехпроводных трехфазных цепях независимо от того, как включены фазы приемника: звездой или треугольником. Такая схема применяется при симметричной и несимметричной нагрузках, причем во втором случае этот метод не дает информации о распределении измеренной мощности между фазами приемника.

Схема включения ваттметров при этом методе приведена на рисунке 33. Как видно из рисунка токовые цепи ваттметров включены в линейные провода А и С, а вольтметровые – на линейные напряжения: 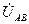первого ваттметра и 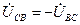второго ваттметра.

Рис. 33

Покажем правильность такого включения ваттметров для случая соединения приемника звездой.

Мгновенная мощность приемника р в общем случае несимметричного приемника

где u_A, u_B, u_C – мгновенные значения фазных напряжений;

i_A, i_B, i_C – мгновенные значения фазных (линейных) токов.

Поскольку для трехпроводной цепи всегда выполняется условие

а, следовательно, i_B = –i_A – i_C, то сделав эту подстановку в (41), получим

Так как разность фазных напряжений является линейным напряжением, то есть u_А – u_В = u_АB; u_C – u_В = u_CB, то

Следовательно, суммарная мгновенная мощность трех фаз оказалась равной алгебраической сумме двух мгновенных мощностей.

Поскольку средняя за период (активная) мощность Р равна произведению действующих значений напряжения и тока, определяющих мгновенное значение мощности, и косинуса угла между их векторами, то средние значения мощностей

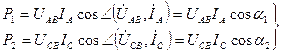где a₁, a₂ – углы сдвига между соответствующими векторами.

Таким образом активная мощность трехфазного приемника равна алгебраической сумме показаний двух ваттметров:

Это означает, что для измерения мощности трехфазного приемника необходимо иметь два ваттметра, которые должны быть включены так, чтобы по их токовым обмоткам протекали токи I_A и I_C, а на вольтметровые обмотки были поданы напряжения U_AB и U_CB, как это показано на схеме рисунка 33.

В общем случае токовые обмотки могут быть включены в любые два линейных провода, но концы вольтметровых обмоток всегда подключаются к свободному проводу.

При симметричной нагрузке, когда I_A = I_B = I_C = I_Ф и φ_A = φ_B = φ_C = φ, то есть Z_a = Z_b = Z_c = Z_Ф = z_Фe^jφ, углы a₁ и a₂ в формуле (46) можно выразить через угол φ сдвига по фазе между фазным напряжением и фазным током. Для этого рассмотрим векторную диаграмму напряжений и токов такого приемника, представленную на рисунке 34 (векторы фазных и линейных токов и напряжений на диаграмме показаны в виде комплексных величин).

Рис. 34

Из диаграммы можно определить, что a₁ = φ + 30°; a₂ = φ – 30°. Тогда показания ваттметров

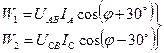
С учетом справедливости в равенствах (47) соотношений U_AB = U_CB = U_Л и I_A = I_C = I_Л можно доказать, что

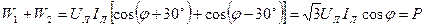то есть сумма показаний двух ваттметров при любых значениях угла φ действительно равна активной мощности Р симметричного приемника (36).

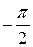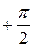Так как угол φ может изменяться в пределах от до , то в соответствии с равенствами (47) значения W₁ и W₂ могут быть как положительными, так и отрицательными. Очевидно показания W₁ и W₂ будут равны друг другу только при активной нагрузке (φ = 0) симметричного приемника, то есть W₁ = W₂ = 0,5P.

При активно-индуктивной нагрузке (φ > 0), когда φ = 60° показание первого ваттметра равно нулю (W₁ = 0), а показания второго ваттметра равно суммарной активной мощности приемника. Покажем, что это действительно так:

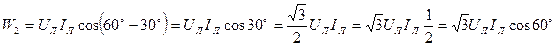где .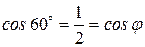

При дальнейшем увеличении угла φ > 60°, показание первого ваттметра W₁ становится отрицательным, то есть активная мощность приемника

Очевидно при активной активно-емкостной нагрузке (φ < 0), если φ = –60°, то W₂ = 0, а при дальнейшем увеличении емкостной составляющей тока показания второго ваттметра становится отрицательным (W₂ < 0).

Следует иметь в виду, что отрицательные значения одной из измеряемых мощностей (W₁ или W₂) могут иметь место и при несимметричной нагрузке.

В цепях трехфазного тока ваттметры используются также для измерения реактивной мощности [6].

Покажем это на схеме включения ваттметра W в фазу А симметричного приемника, соединенного звездой (рис. 35а). Как видно из схемы, по токовой цепи ваттметра протекает ток 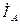, а вольтметровая цепь включена на «чужое» линейное напряжение 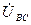, сдвинутое по фазе на 90° относительно «своего» фазного напряжения 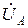, которое использовалось в схеме измерения активной мощности этой фазы.

Соответствующая схеме включения ваттметра (рис. 35а) векторная диаграмма показана на рисунке 35б.

Рис. 35

Как известно [3], измерительный механизм ваттметра электродинамической системы перемножает напряжение на ток и косинус угла a между ними (a = 90° – φ). В рассматриваемом случае это

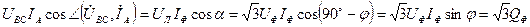то есть увеличенная в 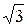реактивная мощность одной фазы симметричного приемника (в данном случае фазы А: Q_Ф = Q_A = U_AI_Asinφ).

Рассмотренный принцип измерения реактивной мощности применяется и при несимметричном приемнике. Это объясняется тем, что в большинстве случаев подаваемые на приемник система линейных и система фазных напряжений, как правило, симметричны [6].

Можно сформулировать следующие правила включения однофазных ваттметров в трехфазные цепи по схемам «с замененными напряжениями»:

1. Токовые обмотки необходимо включать таким же образом, как и при измерении активной мощности.

2. Обмотки напряжения необходимо включать на такие напряжения (линейные или фазные) трехфазной цепи, которые отставали бы на 90° от напряжений, подаваемых на эти обмотки при измерении активной мощности.

На рисунке 36 показана схема измерения реактивной мощности несимметричного приемника методом трех ваттметров, в которой использован принцип измерения реактивной мощности каждой из трех фаз, рассмотренный нами применительно к одной фазе симметричного приемника.

Рис. 36

Каждый ваттметр в этой схеме (рис. 36) измеряет реактивную мощность одной фазы, увеличенную в 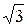раз, поскольку на приборы подаются не фазные, а линейные напряжения U_Л = 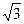U_Ф.

Очевидно суммарная реактивная мощность Q приемника

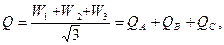
где W₁, W₂, W₃ – показания ваттметров.

Выпускаемые промышленностью трехэлементные ваттметры для измерения реактивной мощности включаются в соответствии со схемой (рис. 36), а необходимость деления на 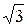вращающего момента измерительного механизма учитывается при градуировке шкалы прибора.

2.5. Электрические измерения как средство анализа цепей

синусоидального тока

Для закрепления теоретического материала раздела курса электротехники «Электрические цепи синусоидального тока» на кафедре «Электромеханические комплексы и системы» университета учебными планами предусмотрено выполнение студентами ряда лабораторных работ.

В частности для студентов механических специальностей в качестве основных планируются лабораторные по исследованию режимов работы цепей однофазного и трехфазного тока.

В программу этих работ включается сборка электрических схем с включением соответствующего набора электроизмерительных приборов, активных и реактивных приемников, регулируемых источников энергии (лабораторных автотрансформаторов), коммутирующих устройств и т.п.

По данным электрических измерений, полученных в процессе выполнения работы, строятся с соблюдением масштабов векторные диаграммы и графики, делаются необходимые расчеты характеристик и параметров цепей.

В качестве примера рассмотрим анализ режимов работы однофазной цепи синусоидального тока с параллельным включением активного, индуктивного и емкостного элементов (r, L и С).

В этой лабораторной работе студенты имеют возможность изучить, каким образом ведет себя каждый из перечисленных элементов, будучи включенным в питающую сеть одиночно или параллельно с двумя другими. Параллельное включение элементов обеспечивает одну и ту же величину напряжения U на каждом элементе, то есть при параллельном соединении приемники работают независимо друг от друга, поскольку изменение тока нагрузки в одной параллельной ветви не влияет на режим работы (величину тока) в других, а изменяется только ток в неразветвленной части цепи.

На рисунке 37 показана разветвленная цепь с параллельным включением резистора с активным сопротивлением r_p, реальной катушки индуктивности, эквивалентная схема которой состоит из условного резистора r_к и идеальной катушки индуктивности L, а также конденсатора, величину емкости которого С можно изменять.

Схема получает питание от лабораторного автотрансформатора АТ (рис. 37), первичная обмотка которого питается от однофазной сети с напряжением U_с = 220В стандартной частоты f = 50Гц.

Рис. 37

Автотрансформатор позволяет плавно регулировать на вторичной стороне величину напряжения от 0 до 250В. Это позволяет во-первых, снизить величину напряжения U (рис. 37) до 100-120В (это значение задается преподавателем) и во-вторых, «отстроиться» от колебаний напряжения в питающей сети U_с, которые могут иметь место в момент снятия показаний электроизмерительных приборов.

Снижение напряжения с U_c = 220В до U = сonst необходимо также для уменьшения тепловыделения резисторов, которые являются основными элементами схем лабораторных установок (снижение «джоулевых потерь» зависит от квадрата подаваемого на резисторы напряжения [2] согласно закону Ленца-Джоуля).

В схеме лабораторной установки (рис. 37) на входе цепи (в неразветвленной ее части) включены четыре прибора: вольтметр V, амперметр А, ваттметр W и фазометр φ, то есть один из приборов оказывается вроде бы лишним (см. раздел 2.3).

Однако это сделано специально по следующим соображениям. Во-первых, студенты на примере фазометра могут познакомиться на практике с устройством измерительного механизма электродинамической системы, построенного по принципу логометра [3]. Во-вторых, при появлении дополнительной информации по измерениям имеется возможность сравнить результаты, полученные вспомогательным расчетом, с результатами непосредственного измерения прибором (например, мощности P, Q, S). В-третьих, наиболее точным результат состояния цепи r, L,C в режиме резонанса можно получить только по показаниям фазометра (при φ = 0).

Рассмотрим режимы работы цепи на рисунке 37 в той последовательности, которая рекомендована программой выполнения лабораторной работы.

В первой части работы исследуется каждая ветвь цепи по отдельности.

Первый режим: замкнут ключ К₁; ключи К₂ и К₃ – разомкнуты. В цепь включен только резистор, по которому течет ток 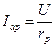, измеряемый амперметром А₁ и общим амперметром А, поскольку оба амперметра включены последовательно. Фазометр показывает угол сдвига φ_а » 0, ваттметр – активную мощность P_W=UI_apcosφ_а. В правильности показаний ваттметра можно убедиться, перемножив показания амперметра и вольтметра (U = const): .

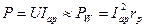Векторная диаграмма для этого режима представлена на рисунке 38а. При этом необходимо задаться масштабом тока 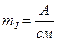, который должен соблюдаться для всех векторов тока при их построении. Как видно из диаграммы вектор тока совпадает по фазе с вектором напряжения 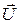, который может показываться без указания масштаба, но одинаковой длины, поскольку он необходим только для того, чтобы ориентировать относительно него векторы токов с учетом углов сдвига φ_а, φ_к и φ_С.

Рис. 38

Обычно общий вектор напряжения 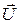(рис. 38) в разветвленной цепи (или тока 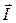в последовательной цепи) принято направлять горизонтально стрелкой вправо, поскольку при вращении векторов относительно центра вращения 0 против часовой стрелки с угловой частотой ω и развертке в графики соответствующих синусоид, синусоида общего вектора напряжения 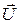будет начинаться с нуля в сторону положительных значений, хотя это совершенно необязательно. Мы сохраним такое расположение векторов, тем более оно было принято ранее [1].

Очевидно в соответствии с диаграммой на рисунке 38а синусоиды напряжения и тока в резисторе будут одновременно проходить все характерные фазы одновременно (положительные и отрицательные амплитуды, прохождение нулевых значений и т.п.).

Второй режим: замкнут ключ К₂; ключи К₁ и К₃ – разомкнуты (рис. 37). В схему включена реальная катушка индуктивности, эквивалентная схема которой состоит из последовательной цепи идеальной индуктивности L и эквивалентного активного сопротивления r_к.

Рассмотрим подробнее эти параметры реальной катушки, которые можно определить только косвенным путем по данным, полученным с помощью измерительных приборов.

В отличие от идеальной катушка (r_к = 0), которая рассматривалась нами ранее, реальная катушка нагревается, причем тепло выделяется не только в обмотке самой катушки, но и в ферромагнитном сердечнике, в котором существуют магнитные потери, выделяемые в виде тепла от вихревых токов и перемагничивания (гистерезиса) [8]. Поэтому ваттметр W, измеряющий активную мощность (необратимо превращающуюся в тепло), измеряет не только мощность джоулевых потерь в самой обмотке 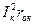(r_oк – активное сопротивление обмотки катушки), но и активную мощность, теряемую в сердечнике. Причем, если положение сердечника внутри катушки изменять, то будет меняться и его доля активной мощности. Поэтому в данной лабораторной работе положение ферромагнитного сердечника не изменяется, что позволяет считать мощность, показанную ваттметром в этом режиме, неизменной при последующих режимах работы рассматриваемой схемы.

В эквивалентную схему реальной катушки (рис. 37) введен условный резистор с сопротивлением r_к, джоулевы потери в котором 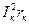создаются реальным током I_к; этим учитывается факт нагревания сердечника, электрически изолированного от самой обмотки, где ток I_к протекает.