Метод непосредственного применения законов Кирхгофа

Этот метод является наиболее общим, поскольку все остальные методы расчета электрических цепей в той или иной степени базируются на использовании законов Кирхгофа.

Задача расчета электрической цепи в классической постановке формулируется следующим образом: заданы структура (схема) цепи, численные значения э.д.с. источников и электрических сопротивлений (проводимостей) всех ветвей, а требуется определить все токи, падения напряжения и мощности всех элементов цепи.

В такой постановке задачи неизвестными являются токи в ветвях. Обозначим буквами: р - общее число ветвей цепи, q - число электрических узлов. Тогда необходимое число уравнений, подлежащих решению, должно быть равно числу ветвей цепи р.

Рис. 24

Рассмотрим в качестве примера электрическую цепь на рисунке 24, в которой число ветвей р = 6, число узлов q = 4. Для расчета такой цепи необходимо составить и решить систему из шести алгебраических уравнений ( по числу ветвей р = 6).

Будем считать, что э.д.с. в схеме (рис. 24) заданы и по величине и по направлению. Что касается токов, то их направления выбираются произвольно (как показано на рисунке 24). Если при расчете токи получатся со знаком минус, то их направление было выбрано неправильно.

Покажем, что число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно q – 1, то есть на одно меньше, чем число узлов q.

В рассматриваемой схеме четыре узла (q = 4). Составим уравнения по первому закону Кирхгофа (см. раздел 1.2) для всех четырех узлов (рис. 24):

для первого узла ;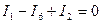

для второго узла ;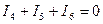

для третьего узла ;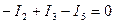

для четвертого узла .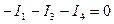

Ток каждой ветви входит в эти четыре уравнения дважды с противоположными знаками, поэтому при суммировании левых частей равенств первых трех узлов получим

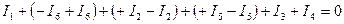, или ,

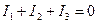то есть уравнение, аналогичное уравнению для четвертого узла.

Таким образом, уравнение для четвертого узла не является независимым, так как оно может быть получено суммированием ранее взятых уравнений для трех узлов.

Распространяя полученный результат на общий случай произвольного числа узлов q, можно сделать заключение, что число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно числу узлов схемы без одного (q – 1).

Поскольку число ветвей р всегда больше числа узлов q, то недостающее число уравнений p – (q – 1) можно составить, пользуясь вторым законом Кирхгофа для замкнутых контуров рассчитываемой цепи.

Чтобы каждое из вновь составляемых уравнений было независимо от предыдущих, необходимо всю схему разбить на независимые контуры.

Независимым называется такой контур, который отличается от остальных контуров хотя бы одной ветвью, принадлежащей только ему.

На рассматриваемой схеме (рис. 24) показаны три таких независимых контура:

p – (q – 1) = p – q + 1 = 6 – 4 +1 = 3.

Действительно: только первому контуру принадлежит ветвь с током I₁; только второму – ветвь с током I₂; только третьему – ветвь с током I₃.

Составим систему из трех уравнений для этих контуров по второму закону Кирхгофа (см. раздел 1.2) с учетом направлений обхода, показанных на рисунке 24:

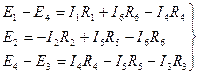
Перепишем первые три уравнения по первому закону Кирхгофа

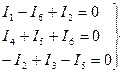
Полученные соотношения (49) и (50) представляют собой систему из шести алгебраических уравнений с шестью неизвестными (токами ветвей в схеме рис. 23), составленных по законам Кирхгофа.

Решив эту систему относительно токов, можно определить напряжения и мощности всех элементов рассматриваемой цепи.