Метод узловых потенциалов. Этот метод, предложенный Максвеллом, позволяет уменьшить число совместно решаемых уравнений до q – 1
Этот метод, предложенный Максвеллом, позволяет уменьшить число совместно решаемых уравнений до q – 1, то есть до числа независимых узлов в схеме цепи.
Метод основан на применении первого закона Кирхгофа и заключается в следующем:
1) один узел схемы принимается базисным с нулевым потенциалом. Такое допущение не изменяет значения токов в ветвях, так как ток в каждой ветви зависит только от разностей потенциалов (напряжений) между узлами, а не от действительных значений потенциалов;
2) для остальных q – 1 узлов составляются уравнения по первому закону Кирхгофа, выражая токи ветвей через потенциалы узлов;
3) решением составленной системы уравнений определяются потенциалы q – 1 узлов относительно базисного, а затем токи ветвей по обобщенному закону Ома (7).
Применение этого метода эффективно при наличии значительного числа ветвей р, включенных между небольшим числом узлов q электрической цепи.
Рассмотрим порядок расчета этим методом применительно к цепи, которая имеет два узла или может быть сведена к таковой после эквивалентных преобразований более сложной цепи. Этот метод получил самостоятельное название – метод двух узлов – и широко применяется при расчете и анализе цепей постоянного и трехфазного тока.
На рисунке 26 показана такая схема с тремя параллельными ветвями (k = 3), в каждую из которых включен источник э.д.с. и резистор. Каждая из ветвей включена между двумя узлами 1 и 2 и находится под одной и той же разностью потенциалов (напряжением U12). Применение метода узловых потенциалов для схемы с двумя узлами (рис. 26) (q – 1 = 2 – 1 =1) требует решения одного уравнения, составленного по первому закону Кирхгофа, независимо от числа параллельно включенных ветвей между узлами 1 и 2.
Примем потенциал узла 2 за базисный и будем считать положительными э.д.с., действующие от узла 2 к узлу 1. Токи ветвей примем также направленными от узла 2 к узлу 1 (на рисунке 26 они не показаны).
Запишем выражения для тока k-той ветви Ik в соответствии с обобщенным законом Ома (7а) и схемой на рисунке 4а.
|
где U12 = –U21 – узловое напряжение цепи (рис. 26);
Еk – э.д.с. k-той ветви;
Rk – сопротивление резистора k-той ветви;
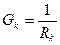– проводимость k-той ветви.
В соответствии с первым законом Кирхгофа для любого из двух узлов справедливо равенство
|
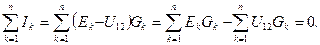
Переписав выражение (55) в виде
,
получим формулу для узлового напряжения цепи U12:
|
.
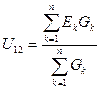Зная узловое напряжение (56), можно рассчитать токи в ветвях по формуле (54).
Для рассматриваемого случая n = 3 (рис. 26):
узловое напряжение
;
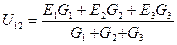токи в ветвях
Дата добавления: 2015-08-01; просмотров: 675;