Расчет проводов линии передачи

Основной задачей расчета линии передачи, соединяющей источник электрической энергии с приемником, является правильный выбор сечения проводов (точнее, площади их поперечного сечения).

Сечение проводов не должно быть завышенным (это приведет к перерасходу проводникового материала) и не должно быть заниженным (это может привести к перегреву проводов и снижению КПД, а также к недопустимой потере напряжения в линии).

Рассмотрим эту задачу применительно к простейшей электрической цепи, состоящей из идеального источника энергии постоянного тока, двухпроводной линии передачи и приемника (нагрузочного резистора). Схема цепи показана на рисунке 33.

На схеме рисунка 33 приняты обозначения:

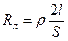- сопротивление линии (обоих проводов); r - удельное сопротивление материала проводов; l – длина одного провода (расстояние между источником э.д.с. Е и приемником R_н); S – площадь поперечного сечения провода;

R_л/2 – сопротивление одного провода;

R_н –сопротивление резистора (нагрузки);

Е – э.д.с. идеального источника (R_вт = 0);

U₁ = E - IR_Вт = Е – напряжение в начале линии, равное э.д.с. идеального источника;

U₂ - напряжение в конце линии (на приемнике U₂ = IR_н);

I – ток в рассматриваемой цепи.

При расчете линии передачи обычно заданы: напряжение U₁ = Е = const источника электроэнергии; расстояние l от источника до потребителя; сила тока I и напряжение U₂ = U_н (номинальное напряжение приемника).

Задачей расчета является выбор такого сечения проводов, при котором обеспечивается нормальное рабочее напряжение на приемнике U₂.

,

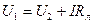где 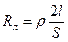, 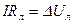- потери напряжения в линии.

Сделав соответствующие подстановки в (70), получим искомое сечение:

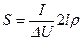то есть сечение обратно пропорционально допустимой потере напряжения ΔU.

При расчете и анализе линий с различным уровнем напряжения используют понятие относительной потери напряжения

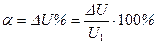
Из равенства (72) следует

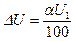Подставим (73) в (71):

Умножив числитель и знаменатель правой части на напряжение U₁, получим

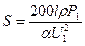где Р₁ = U₁I – мощность, передаваемая источником энергии через линию передачи приемнику.

Из равенства (75) следует очень важный вывод: при заданных значениях α (относительной потери напряжения) и передаваемой мощности Р₁, сечение проводов S обратно пропорционально квадрату напряжения.

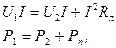
где Р₁ = U₁I = ЕI – мощность, развиваемая идеальным источником энергии (у которого

КПД η_и = 100%);

Р₂ = U₂I – мощность, потребляемая приемником;

Р_п = I²R_л – потеря мощности в линии передачи.

Очевидно все энергетические характеристики линии передачи аналогичны соответствующим характеристикам реального источника э.д.с., представленным на рисунке 32.

При расчете сечения проводов линии передачи по допустимой величине ΔU с использованием формулы (71) 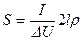необходимо сделать проверку проводов на допустимость их работы по условиям нагревания.

Подробный расчет сечения проводов по условиям нагревания в настоящее время не практикуется, поскольку существуют стандартные таблицы нормированных нагрузок проводов током для различных типов проводов и разных условий их работы. Как правило, нагрузку проводов в этих таблицах характеризуют не величиной тока I, а плотностью тока δ = I/S [А/мм²]. Допустимая плотность тока зависит от величины сечения S проводника и от условий его охлаждения.

Поэтому после выбора стандартного сечения провода из условий допустимой потери напряжения этот провод проверяют по условиям нагревания в соответствующих таблицах. Если это условие не выполняется, то берется следующее большее стандартное сечение, удовлетворяющее условиям нагревания.

Очевидно в этом случае потеря напряжения в линии уменьшается, то есть повышается качество передачи энергии по этому показателю.

Список литературы

1. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. – СПб.; М.: «Лань», 2005.

2. Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. – М.: «Энергоатомиздат», 1995.

3. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. – М.: «Высшая школа», 1978.

4. Касаткин А.С., Немцов М.В. Электротехника. – М.: «Академия», 2007.

5. Савельев И.В. Курс общей физики. Том 2. – М.: «Наука», 1982.

6. Электроизмерительные приборы. Методические указания. Сост. Б.В. Рудаков, А.Г. Филимонов. – СПб.: ПГУПС, 2005.

7. Расчет цепей постоянного и однофазного переменного тока. Методика решения типовых задач. Сост. А.И. Хожаинов, Б.В. Рудаков, Б.А. Тимофеев, А.Г. Филимонов. – СПб.: ПГУПС, 2000.

Основные законы электротехники и методы расчета электрических цепей

(методическое пособие для студентов заочного факультета)

Предназначено для студентов неэлетротехнических специальностей, изучающих учебную дисциплину «Электротехника и электроника»

Составители: Рудаков Борис Владимирович

Филимонов Аркадий Григорьевич

Рецензент: доцент Б.А. Трифонов

Компьютерная верстка и техническое редактирование: Н.А. Ведерникова

Подписано в печать с оригинал-макета 04.09.2007

Отпечатано в авторской редакции

Тираж 300 экз.

* Единицы измерения физических величин, названные в честь ученых, обозначаются заглавной буквой.

* В дальнейшем рассматривается линейная магнитная цепь, для которой все ферромагнитные участки работают на линейной части магнитной характеристики соответствующего ферромагнитного материала.

* Синусоидальные функции времени принято записывать и строить их графики в зависимости от фазового угла ωt, где ω = 2p/T = 2pf = const – угловая частота [радиан/c]

* Напомним, что последующие рассуждения будут справедливы только для идеального трансформатора, работающего на нагрузочный резистор с сопротивлением R_н.

* В реальном трансформаторе (с учетом потерь напряжения в первичной обмотке при увеличении нагрузки) условие Φ _m0 = const сохраняется с незначительной погрешностью.

* Источники тока в настоящей работе не рассматриваются.

* На рисунке 25а это не сделано, чтобы не усложнять изображение схемы.

* В механике принцип наложения применяется, например, при анализе движения тела под действием нескольких сил (как результат сложения движений, вызываемых каждой силой в отдельности).