Энергетические соотношения в простейшей цепи

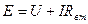
Такое же уравнение было получено из закона Ома для замкнутой цепи (4). Таким образом: закон Ома для замкнутой цепи можно рассматривать как частный случай второго закона Кирхгофа (поскольку цепь простейшая: с одним источником э.д.с. и не имеет электрических узлов).

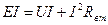
или

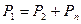где 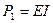- мощность, развиваемая источником энергии;

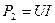- мощность, потребляемая приемником;

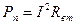- потеря мощности в источнике энергии.

Очевидно уравнения (61) и (62) являются законом сохранения энергии применительно к рассматриваемой цепи. Поскольку этот закон выражается в единицах мощности, то он получил название «баланс мощностей» (см. раздел 2.7) и может быть сформулирован следующим образом: мощность, развиваемая источником энергии, равна сумме мощностей, потребляемой приемником и теряемой в самом источнике в виде тепловых («джоулевых») потерь.

Введем понятие о коэффициенте полезного действия (КПД) источника энергии η как отношение полезной мощности Р₂ (потребляемой приемником) к затраченной мощности Р₁ (развиваемой источником):

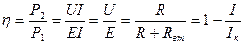
В выражении (63) КПД реального источника всегда меньше единицы η < 1,0. Если КПД выражается в процентах, то

.

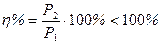Очевидно КПД идеального источника э.д.с. (R_вт = 0, U = Е) η_ид% = 100% или η_ид = 1,0 (в долях единицы).

Рассмотрим энергетические характеристики реального источника э.д.с. в зависимости от тока I нагрузки на всем диапазоне его изменения от I = 0 до I = I_к = Е/R_вт (рис. 32).

Рис. 32

Из выражения мощности приемника Р₂ = UI можно убедиться, что эта мощность дважды обращается в ноль: в режиме холостого хода, когда I = 0, и в режиме короткого замыкания, когда U = 0. Следовательно, зависимость Р₂ = F(I) в диапазоне изменения тока от 0 до I_к имеет максимум.

Для определения условий, при которых эта мощность будет наибольшей (Р₂ = Р_2max) воспользуемся уравнением (61)

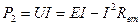
Возьмем производную 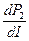и приравняем ее нулю

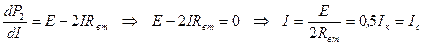то есть приемник потребляет максимальную мощность при согласованном режиме, когда R = R_вт и ток I = I_с = 0,5I_к.

Выразим мощность приемника Р₂ = UI = I²R, подставив в правую часть ток 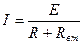(закон Ома для замкнутой цепи):

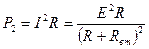Поскольку максимальная мощность приемника (в согласованном режиме) наступает при R = R_вт , то сделав эту подстановку в (66), получим

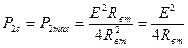Мощность, развиваемая источником энергии в согласованном режиме с учетом (65):

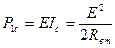Наибольшую мощность Р_1max источник энергии развивает при коротком замыкании :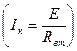

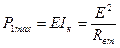
Коэффициент полезного действия η источника э.д.с., как следует из равенства (63), представляет собой линейную зависимость от тока нагрузки. В зоне малых токов он близок к единице, а при коротком замыкании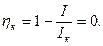

В согласованном режиме 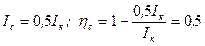, то есть КПД источника равен 50%.

Из-за такого низкого КПД согласованный режим в промышленных установках не применяется. Его применяют в слаботочных цепях (схемы автоматики, связи, электрических измерений), в которых КПД не имеет решающего значения, а есть необходимость получить от источника наибольшую мощность.

Развиваемая источником энергии мощность P₁ = EI линейно зависит от тока нагрузки, а потери в источнике – от квадрата тока Р_п = R_втI².

В режиме короткого замыкания 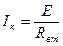вся мощность, развиваемая источником, выделяется в самом источнике 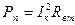в виде тепловых («джоулевых») потерь, поэтому КПД источника равен нулю: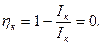

Для большинства промышленных источников электроэнергии расчетный КПД в номинальном режиме принимается значительно больше, чем в согласованном режиме, и составляет η = 0,8¸0,9. соответственно номинальный ток составляет I_н = (0,1¸0,2)I_к.

Рассмотренные энергетические характеристики представлены на рисунке 32.