В трехфазной схеме, соединенной звездой 4 страница

Наличие факта нагревания реальной катушки (самой обмотки и сердечника) и появления в эквивалентной схеме резистора r_к свидетельствует о том, что угол сдвига по фазе φ_к будет меньше 90°, что и подтверждается показаниями фазометра и ваттметра P_W » UI_кcosφ_к, что можно опять-таки проверить, сравнив прямые измерения P_W с результатами расчета по показаниям вольтметра, амперметра и фазометра.

На рисунке 38б приведена векторная диаграмма цепи с реальной катушкой, на которой вектор тока 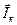под углом φ_к, измеренным фазометром, с помощью транспортира пристраивается к началу вектора напряжения. Пунктиром показано условное разложение вектора 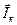на активную составляющую 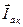, совпадающую с вектором напряжения 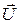, и реактивную 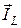, отстающую от напряжения на угол 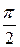, как в идеальной катушке. 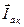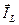Следует помнить, что эти токи и реально измерены быть не могут. Очевидно 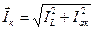. По данным измерений тока и напряжения полное сопротивление катушки , а с учетом показаний ваттметра или фазометра можно определить и параметры эквивалентной схемы катушки (рис. 37). Активное сопротивление катушки 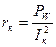или r_к = z_кcosφ_к. Соответственно индуктивное сопротивление катушки 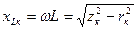, а следовательно, индуктивность 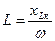, где 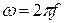(f = 50Гц).

Кстати, если известно сопротивление обмотки катушки r_ок (его можно измерить постоянным током методом амперметра – вольтметра), то можно выделить долю активного сопротивления в условном активном сопротивлении 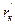эквивалентной схемы r_к: 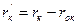. Этот параметр остается неизменным, если положение сердечника внутри катушки не изменяется.

Третий режим: замкнут ключ К₃; ключи К₁ и К₂ – разомкнуты. Включен конденсатор. Амперметры А и А₃ показывают величину тока 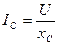, где 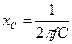. Фазометр показывает угол φ » –90° (обычно 88–90°), ваттметр P_W » 0, поскольку P = UIcosφ_C » 0. Векторная диаграмма представлена на рисунке 38в, из которой видно, что ток в емкости опережает напряжение на 90°.

Вторая половина данной лабораторной работы предполагает совместное включение трех параллельных ветвей (рис. 37) и изменение одного из параметров, а именно емкости С, поскольку в цепи конденсатора угол сдвига φ_C » –90° практически остается одним и тем же по величине независимо от силы тока. Ток I_C можно менять, переключая с помощью тумблеров схему батареи конденсаторов.

Четвертый режим: включены все три ключа, но емкость С = 0 (выключены все тумблеры, или просто разомкнут ключ К₃ на схеме рис. 37).

Амперметры А₁ и А₂ показывают те же токи, что и в первых двух режимах, поскольку напряжение U » const, сопротивление резистора r_p и сопротивление катушки z_к во всех режимах остается неизменным.

На рисунке 39 векторы 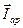и 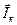построены в том же масштабе, как и на рисунках 38а и 38б, совмещенными с началом вектора 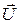, то есть с центром вращения векторов 0. Суммарный вектор тока 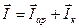построен по правилу треугольника. Угол φ, измеряемый фазометром, является отстающим, причем φ < φ_к, поскольку увеличилась активная составляющая общей цепи за счет резистора (цепь имеет индуктивный характер).

Ваттметр W показывает суммарную активную мощность резистора и катушки .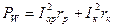

Пятый режим – резонанс токов. Включив ключ К₃, с помощью включенных тумблеров батареи конденсаторов увеличивают с нуля ток I_C в конденсаторе до такой величины, чтобы стрелка на фазометре установилась на нуле φ = 0 (этому режиму соответствует величина емкости С = С_рез). Ваттметр в режиме резонанса показывает ту же величину активной мощности, как и в предыдущем режиме, поскольку конденсатор – это практически идеальный реактивный приемник (φ_C » –90°). Как известно [1], при резонансе токов суммарный ток в неразветвленной части цепи должен быть наименьшим.

На рисунке 40 показаны слагаемые векторы 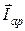, , 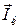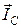и построена векторная диаграмма с учетом первого закона Кирхгофа: .

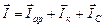Рис. 40

Поскольку в режиме резонанса должно выполняться условие 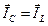(рис. 38б и 38в), то, как видно из диаграммы (рис. 40), суммарный ток I состоит только из тока резистора 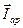и тока активной составляющей тока катушки 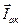: 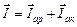. Таким образом из-за отсутствия реактивной составляющей суммарный ток действительно имеет наименьшее значение.

В этом можно еще раз убедиться, рассмотрев следующий режим, при котором I_C > I_L (С_макс > C_рез).

Шестой режим: режим максимальной емкости, при котором цепь на выходных зажимах имеет емкостный характер: ток опережает напряжение (фазометр показывает угол сдвига φ < 0).

Соответствующая этому режиму векторная диаграмма показана на рисунке 41а. На векторной диаграмме (рис. 41б) выделен штриховкой векторный треугольник токов с показом разложения вектора тока катушки I_к на активную I_ак = I_кcosφ_к и реактивную I_L = I_кsinφ_к составляющие.

Рис. 41

Катеты этого прямоугольного треугольника: прилежащий к углу φ: I_ар + I_ак, противолежащий: I_c – I_L. Гипотенуза треугольника . Поскольку по условию резонанса токов [1] b_c – b_L = 0, или I_C – I_L = 0, то при резонансе 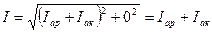, то есть ток в неразветвленной части цепи становится наименьшим, как уже упоминалось выше.

По данным второй части рассматриваемой лабораторной работы строится графическая зависимость I = F(C) тока в неразветвленной части цепи I от величины емкости при неизменной величине токов в резисторе и катушке. Выше мы рассмотрели три режима: С = 0, С = С_рез, С = С_макс. Обычно в лаборатории снимают пять режимов, включая два промежуточных: 0 < С < С_рез и С_рез < С < С_макс. Примерный вид такого графика для пяти измерений показан на рисунке 42.

Список литературы

1. Электрические цепи синусоидального тока. Методическое пособие для студентов заочной формы обучения. Часть 1. Сост. Рудаков Б.В., Филимонов А.Г. – СПб.: ПГУПС, 2010.

2. Основные законы электротехники и методы расчета электрических цепей. Методическое пособие для студентов заочного факультета. Сост. Рудаков Б.В., Филимонов А.Г. – СПб.: ПГУПС, 2007.

3. Электроизмерительные приборы. Методические указания для студентов заочной формы обучения. Сост. Рудаков Б.В., Филимонов А.Г. – СПб.: ПГУПС, 2008.

4. Электрические цепи трехфазного тока. Методические указания для выполнения курсовой работы по дисциплине «Электротехника и электроника» для студентов механических специальностей заочной формы обучения. Сост. Васильев П.Ю., Рудаков Б.В., Филимонов А.Г. – СПб.: ПГУПС, 2005.

5. Методика решения типовых задач по расчету цепей трехфазного тока. Методические указания. Сост. Хожаинов А.И., Рудаков Б.В., Филимонов А.Г. – СПб.: ПГУПС, 2000.

6. Измерение активной и реактивной мощности в цепях трехфазного тока. Методические указания к лабораторной работе. Сост. Рудаков Б.В., Рябинин Г. А. – СПб.: ПГУПС, 1996.

7. Расчет и анализ сложной трехфазной цепи символическим методом. Методические указания для выполнения курсовой работы. Сост. Рудаков Б.В., Трифонов Б. А. – СПб.: ПГУПС, 2003.

8. Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. – М.: Энергоатомиздат, 1985.

9. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. – СПб., М.: Лань, 2005.