Доказательство. Введем подвижную систему отсчета с началом в центре масс С, движущуюся поступательно относительно основной инерциальной системы отсчета

Введем подвижную систему отсчета с началом в центре масс С, движущуюся поступательно относительно основной инерциальной системы отсчета. Представим скорость n-й МТ, входящей в СМТ, относительно основной системы отсчета в виде (Ч.1 Кинематика):

,
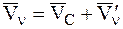где 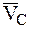– скорость движения центра масс СМТ, а – скорость n-й точки СМТ по отношению к подвижной системе отсчета.

Подставив это выражение в соотношение (4.30), получим:

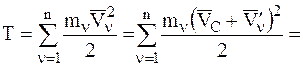
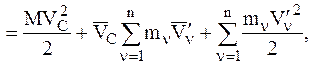(4.42)

где 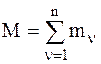– масса всей системы, 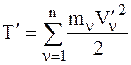– кинетическая энергия СМТ при ее движении относительно подвижной системы отсчета, перемещающейся вместе с центром масс поступательно.

На основании соотношений (4.6) и (4.16) для суммы во втором слагаемом правой части выражения (4.42) можно записать:

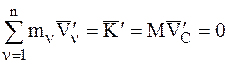, так как .

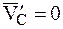Из соотношения (4.42) имеем теорему Кенига:

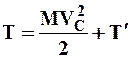. (4.43)