Возвращаясь к стандартной схеме
V = f (x, 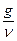 )
)
или
m0 L t-1 = Lα (L-1 t-1)β.
Система в данном случае будет определенной и имеет вид
α – β = 1,
β = 1.
Окончательно α = 2, β = 1 и
V = 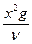 .
.
Таким образом, выбрав новый, комбинированный параметр, получим определенную систему и ее точное решение.
Если параметр выбрать в виде
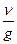 , то
, то 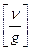 = L t,
= L t,
то
V = f (x, 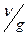 )
)
или
m0 L t-1 = Lα (L t)β.
Система будет иметь вид
α + β = 1, β = -1.
Окончательно β = -1, α = 2 и
V = 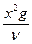 .
.
Приходится сделать вывод, что существует значительное число задач, для решения которых метод анализа размерностей требует особого искусства для своего применения.
Пример Д.1.7. Через короткую трубку небольшого радиуса r выдули мыльный пузырь радиусом R >> r и закрыли конец трубки. Если затем открыть ее конец, то пузырь начнет уменьшаться и, наконец, совсем сдуется. Указать вид зависимости для времени жизни T такого пузыря.
Вначале дадим качественные оценки процесса. Очевидно, что искомое время T тем больше, чем больше радиус R пузыря. С другой стороны, это время тем меньше, чем больше коэффициент поверхностного натяжения σ мыльной пленки – могут быть разные сорта мыла (если σ представить очень малым, то пузырь будет сдуваться очень долго). Очевидно также, что чем меньше радиус трубки, тем время T больше. По закону сохранения энергии, в процессе сдувания пузыря его потенциальная поверхностная энергия переходит в кинетическую выходящего воздуха (кинетическая энергия самого пузыря мала).
Таким образом, имеем следующие параметры, которые заданы и которые обязательно требуется учесть: радиус пузыря R, радиус трубки r, коэффициент поверхностного натяжения σ. Если теперь представить общую зависимость для T, то она должна была бы иметь вид
T = f (R,r,σ),
что заведомо неправильно, так как в σ входит масса, а в левую часть последнего равенства масса не входит.
В данном случае метод анализа размерностей подсказывает, что в правую часть должна входить плотность газа, которым был надут пузырь, в данном случае – плотность воздуха ρ. Можно поэтому заключить, что если пузырь надут водородом, то он сдуется быстрее такого же, но надутого воздухом.
В окончательном виде зависимость для T представится так
T = f (R,r,σ, ρ).
Учитывая Замечание Д.2, из σ и ρ возможно сформировать параметр 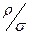 (чем больше σ, тем время жизни пузыря меньше и σ находится в знаменателе, а ρ в числителе; σ и ρ входят поэтому в одинаковых по абсолютной величине, но разных по знаку степенях). Размерность этого параметра
(чем больше σ, тем время жизни пузыря меньше и σ находится в знаменателе, а ρ в числителе; σ и ρ входят поэтому в одинаковых по абсолютной величине, но разных по знаку степенях). Размерность этого параметра
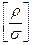 =
= 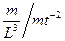 = L-3 t2.
= L-3 t2.
Основная функциональная зависимость представится в виде
T = c · 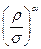 ·Rβ ·rγ
·Rβ ·rγ
или
m0 L0 t = (L-3 t2 )α L βL γ.
Система уравнений для α, β и γ примет вид
γ + β – 3α = 0, 2α =1
или
α =  , 2α + 2β = 3.
, 2α + 2β = 3.
Учитывая замечания к данной задаче о качественных особенностях процесса, можно установить, что r должен находиться в знаменателе, а R в числителе основной зависимости и поэтому γ<0, β>0. Для выбора решений уравнения 2γ+2β = 3 можно предложить перебор целочисленных значений γ; например, при γ = -1 получим, что β = 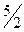 , при γ = -2, ρ =
, при γ = -2, ρ = 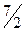 и т.д. Для выбора решения допустим, что для трубки характерна ее площадь – тогда γ = -2 и ρ =
и т.д. Для выбора решения допустим, что для трубки характерна ее площадь – тогда γ = -2 и ρ = 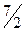 .
.
Окончательно зависимость для T примет вид
T = c 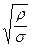 ·
· 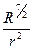 .
.
Дата добавления: 2015-08-01; просмотров: 693;
