Примеры из гидравлики

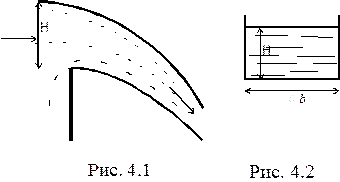Пример 4.1.Установить зависимость расхода жидкости, протекающей через водослив, от напора H на водосливе и его ширины b. Из опытов известно, что расход пропорционален первой степени b.

Водослив, по определению, представляет собой преграду, через которую переливается вода и в простейшем случае может быть представлен в виде вертикальной стенки (рис. 4.1). По форме отверстие водослива, через которое протекает вода, может быть, в частности, прямоугольным, как показано на рис. 4.2. В процессе течения через водослив потенциальная энергия жидкости преобразуется в кинетическую в поле силы тяжести и поэтому в зависимость для расхода должно входить ускорение g; в результате для расхода имеем:

Q=Cb^a g^b H^g,

что приводит к системе, из которой, учитывая, что a=1, получаем:

Q=Cb 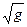H .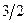

Обычно применяется зависимость для расхода через водослив, которая имеет вид:

Q=m b 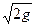H 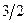, (4.1)

где m- коэффициент расхода водослива.

Задача 4.1.Определить зависимость скорости звука в газе от абсолютной температуры Т.

Решение.Скорость звука есть скорость распространения волн сжатия и разряжения в упругой среде. Так как эта скорость значительна, то соседние участки газа, в котором проходит волна, не успевают обмениваться теплом (при сжатии и расширении). Поэтому процесс распространения звука можно считать адиабатическим. При этом очевидно, что эта скорость зависит от упругих свойств газа, которые определяются уравнением, связывающим плотность и давление, то есть

.

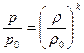Поэтому скорость звука представится в таком виде

,

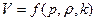где k – показатель адиабаты для данного газа.

Предполагается, что скорость звука не зависит ни от амплитуды (силы звука), ни от частоты звуковых колебаний. Далее, действуя по известной схеме, получим

,

где j(k) – некоторая неизвестная функция от k. Согласно уравнению состояния p/r=RT и поэтому

,

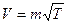где m – размерный коэффициент, зависящий от R и k, т.е. от рода газа.

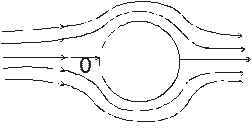Задача 4.2.Плоский поток идеальной несжимаемой жидкости обтекает бесконечный цилиндр (рис.4.3). Скорость потока далеко от цилиндра равна V, а давление в потоке там же равно нулю. Давление в точке О равно p (точка О называется передней критической точкой и скорость в ней равна нулю). Найти вид зависимости p от V.

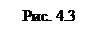Решение.Искомое давление зависит от плотности жидкости ρ, от радиуса цилиндра R

p=f(ρ, V, R).

Окончательный результат имеет вид

p=CρV².

Задача 4.3.Жидкость тонкой плёнкой стекает по вертикальной стенке под действием силы тяжести. Определить вид зависимости для скорости стекания пленки.

Решение.Будем считать жидкость реальной (вязкой), не учитываем силы поверхностного натяжения, тем самым предполагая, что пленка достаточно толстая (порядка долей миллиметра) и течение происходит под действием силы тяжести, а тормозящей силой является сила трения, обусловленная вязкостью жидкости. Можно представить, как стекают по стенке пленки одной и той же жидкости, но разной толщины – поэтому может быть сделан вывод, что в число параметров должна войти толщина пленки 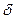. Причем из опыта следует, что чем толщина пленки больше, тем больше скорость стекания. Если стекают пленки двух различающихся по вязкости жидкостей, например, воды и глицерина, то скорость будет больше у пленки жидкости, чья вязкость будет меньше, т.е. пленка воды стекает быстрее, чем глицерина (при одинаковой толщине). Следовательно, в зависимость для скорости должна входить вязкость 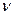. Так как основной движущей силой является сила тяжести, то в выражение для скорости должно войти и ускорение силы тяжести g. В число параметров помимо названных не может быть включена плотность жидкости r (или она может войти вместе с одинаковыми коэффициентом вязкости 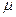в виде 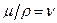, чтобы исключить размерность массы в правой части).

Основываясь на приведенных рассуждениях, возможно представить соотношение для скорости в виде

.

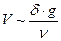Размерность левой части [Lt^-1], а размерность правой [t^-1], поэтому для соблюдения правила размерностей необходимо правую часть умножить на L (т.е. на 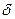) и окончательно получаем соотношение

,

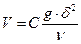которые в данном случае выведено нами элементарно.

Решим данную задачу методом анализа размерностей. Учитывая сделанные в начале решения замечания о входящих в общее соотношение параметрах, возможно представить общий вид зависимости для скорости так

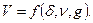
В данном случае можно заранее предполагать, что число уравнений будет меньше числа неизвестных: в размерности скорости присутствуют длина и время – т.е. будет 2 уравнения, а в правой части 3 параметра.

Применяя стандартную схему решения, получим

,

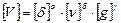или

.

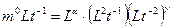Получим в результате систему уравнений

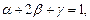
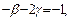
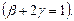
Ищем наиболее простое решение при , тогда .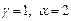

Окончательно имеем

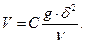
Решение можно упростить, если ввести параметр 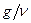, по своему смыслу отражающий отношение силы тяжести, действующей на стекающую пленку к силе трения. Параметр 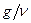имеет размерность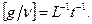

Основная зависимость для скорости примет вид

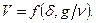
Применяя стандартную схему, получим

.

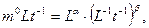Система уравнений будет такая

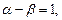
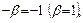
откуда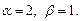

Окончательный результат имеет вид

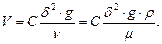
В данном решении введение параметра 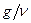сделало систему уравнений определенной и позволило весьма корректно применить метод анализа размерностей.

Для сравнения, подчеркивая простоту и доступность метода анализа размерностей, решим данную задачу точно. Для этого заметим, что обычно в тонких стекающих пленках имеет место ламинарный режим течения и точное решение для скорости возможно получить, решая уравнение Навье- Стокса.

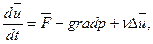
где 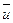– вектор скорости; 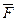– вектор ускорения внешних массовых сил; p – гидродинамическое давление, 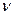– кинетический коэффициент вязкости; 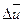– оператор Лапласа вектора скорости. Представив уравнение Навье-Стокса в виде проекций на прямоугольные координаты x, y, z, получим

,

,

.

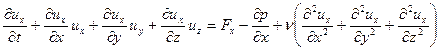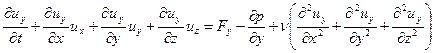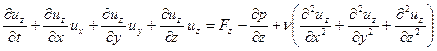Считаем течение плоским, поэтому вдоль оси y никакие параметры не меняются – вследствие этого второе уравнение системы исключается из рассмотрения.

Считаем движение установившимся, поэтому

.

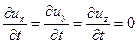Составляющие ускорения внешней массовой силы равны

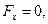
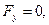
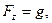
где g – ускорение свободного падения.

Составляющая скорости 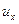во всех точках равна нулю, так как движение плоское (в плоскости рисунка - одномерное). Составляющей скорости, отличной от нуля, является, как это следует из рисунка, 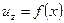. Поэтому из первого уравнения следует

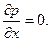
Из третьего уравнения следует

,

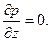так как поток (стекающая пленка жидкости) граничит с атмосферой (с областью постоянного давления).

Из третьего уравнения системы также следует

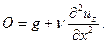
Так как 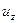зависит только от x, последнее уравнение может быть записано в виде

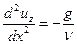или .

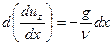Интегрируя последнее уравнение, получим

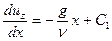или ,

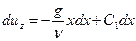интегрируя в свою очередь полученное уравнение, имеем

.

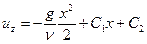Определим произвольные постоянные С₁ и С₂. Очевидно, что на стенке при x=0 скорость равна нулю, т.е. 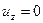. Подставляя в выражение для 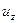значение x=0, определим С₂: С₂=0.

В данном случае (как и в любом ламинарном потоке) выполняется для касательного напряжения

.

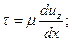Касательное напряжение на поверхности жидкой пленки равно нулю: 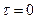, так как она граничит с атмосферой. Поэтому на свободной поверхности

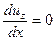при .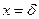

Дифференцируя по x обе части выражения для распределения скорости и подставляя вместо x толщину пленки 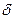, получим

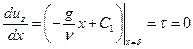, откуда .

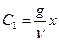С учетом известных теперь значений С₁ и С₂ выражение для 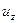будет иметь вид

.

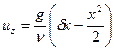Расход жидкости в потоке единичной ширины равен

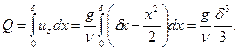
Окончательно, средняя скорость течения пленки равна

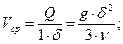
Это выражение и является точным решением для скорости стекания пленки (из него следует, что постоянная С в выражении, полученном методом анализа размерностей, равна ).

Если наклонить стенку на угол 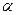к горизонту, то закон распределения скоростей по глубине будет иметь вид

.

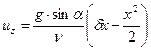Последняя формула выражает также распределение скоростей при ламинарном течении в открытом канале в потоке конечной глубины.

Задача 4.4.Найти зависимость скорости звука в твердой среде от свойств этой среды.

Решение.Звук представляет собой колебания и поэтому скорость его распространения зависит от упругих свойств самой среды; например, от модуля упругости Е. Предполагаем, что скорость звука V зависит только от свойств среды, а не от характеристик звуковых колебаний. В размерность модуля упругости входит масса и для получения в левой части размерности скорости включаем в правую часть искомой зависимости плотность как величину, содержащую массу (вхождение плотности в зависимость для скорости не так очевидно, как модуля упругости).

Искомая зависимость

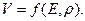
Учитываем, что [ρ]=mL^-3, [V]=Lt ^-1, [E]=mL^-1t ^-2.

Окончательный результат имеет вид

.

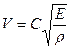Задача 4.5. Найти зависимость для превышения давления 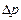при гидравлическом ударе.

Решение. При изменении скорости в сечении напорного трубопровода давление в нем также изменяется. Это явление называется гидравлическим ударом и служит примером неустановившегося движения, например, открытие или закрытие крана, остановка или начало работы насоса и т.д. Главной задачей при рассмотрении гидравлического удара является определение превышения давления в трубопроводе. Решать эту задачу логично, применяя известное из механики уравнение

.

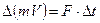Принимаем 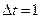и учитываем, что для потока жидкости в трубе 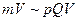, где p – плотность жидкости; Q – расход (Q=const); V – скорость.

Рассмотрим наиболее простой случай, когда труба практически мгновенно перекрывается задвижкой; при этом, начиная с частиц жидкости вблизи задвижки, вся жидкость останавливается. Область, где жидкость останавливается (от скорости V до V=0), распространяется с некоторой конечной скоростью с против направления течения. Так как основной причиной изменения давления при гидравлическом ударе является изменение скорости, то при поиске зависимости для 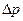в правую часть ее должна войти скорость. Поскольку в 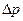входит и масса, то и в правую часть зависимости должна войти масса; поэтому в число аргументов включаем плотность. Таким образом

.

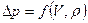После применения стандартной схемы получим 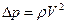. Учитывая, что на величину 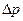влияет скорость распространения возмущений, правильный результат запишется в виде

,

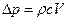где с – скорость распространения возмущений. Вхождение скорости движения жидкости (средней скорости V) в первой степени в зависимости для 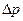следует также из уравнения сохранения количества движения .

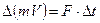Пример 4.2. Рассмотреть зависимость для скорости распространения гравитационных волн на поверхности воды.

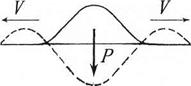
Волны – это распространяющиеся колебания; в положении равновесия поверхность воды представляет горизонтальную плоскость. Если каким-то образом вывести из положения равновесия хотя бы незначительную часть поверхности воды, например, бросить камень, то это «возмущение» будет распространяться в виде волны. В данном случае колебания поверхности являются результатом взаимодействия двух факторов: силы, возвращающей в положение равновесия, и инерции, заставляющей проскакивать это положение равновесия.

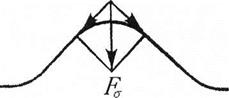
Если на поверхности жидкости образуется «горб» (возвышение), то вернуть частицы жидкости в положение равновесия может, например, сила тяжести Р (рис.4.5), пропорциональная ускорению свободного падения g. Двигаясь вниз, по инерции «горб» пройдет ниже положения равновесия; рядом Рис. 4.5

с ним будет вытеснен другой «горб» и т.д., в результате чего побежит волна, характеризуемая некоторой скоростью V и длиной 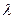(расстоянием между «горбами»). Величину P необходимо учесть, так как от P зависит вес «горба», т.е. возвращающая сила. Заметим, что колебания происходят в вертикальной плоскости, а волны распространяются в горизонтальной, поэтому они являются поперечными волнами.

Таким образом, движение волны по поверхности жидкости описывается следующими величинами

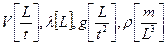
и общий вид зависимости для скорости будет таким

.

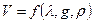Применяя стандартную схему, получим для скорости V

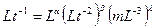или

по L: 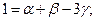по t: 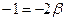; по m: .

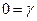Решая эту систему, получим

В результате зависимость для скорости распространения волн имеет вид

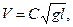
точное решение

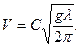
В конечный результат для V не вошло значение плотности р (сам метод анализа размерностей указал нам на этот факт). С точки зрения физики явления это произошло потому, что вес «горба», увлекающий его вниз, и его масса, определяющая инерционность, пропорциональны. Аналогичный случай имел место при выводе зависимости для периода колебаний математического маятника

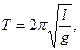
- период Т также не зависит от массы, подвешенной на нити длиной .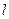

При использовании зависимости для скорости распространения волн V необходимо иметь в виду следующее:

а) если длина волны значительно меньше глубины того водоема, где они распространяются («глубокая вода»), то за 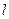принимается длина волны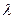

;

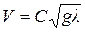б) если длинные волны (в том смысле, что их длина значительно больше их амплитуды) распространяются на глубине h, соизмеримой с их длиной, то скорость их распространения V не может превышать величины

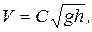
где вместо 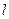принимается глубина потока.

Решенная нами задача относится к так называемым гравитационным волнам, в распространении которых первостепенное значение имеет сила земного притяжения.

Если же волны становятся очень мелкими (волны «ряби») - их можно наблюдать в кювете с водой при возмущении поверхности воды иголкой, - то «горб» стремится вернуть в положение равновесия Рис. 4.6 другая сила - сила поверхностного натяжения, связанная с коэффициентом поверхностного натяжения 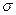(рис.4.6). В этом случае скорость распространения волн V_n будет зависеть от величин

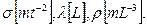
Применяя стандартную схему, получим для скорости V_n

,

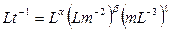или

решаем последнюю систему:

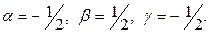
Зависимость для скорости V_n имеет вид

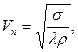
или, согласно точной теории

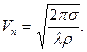
Задача 4.6.Образовать безразмерный критерий, определяющий состояние открытого равномерного потока.

Решение.Движение жидкости происходит под действием силы тяжести, поэтому в критерий обязательно должно войти ускорение свободного падения g. Далее, для того, чтобы критерий был безразмерным, необходимо в него включить скорость потока (скомпенсировав тем самым время, входящее в g). На основе анализа размерностей окончательно решаем, что должен войти в критерий некоторый линейный параметр и форма критерия такова (он называется числом Фруда)

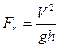(допустимо и ),

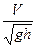где V – средняя скорость потока; h – глубина потока.

При F_r>1 поток называется бурным, при F_r<1 – спокойным. Физический смысл числа Фруда может быть пояснен так: из примера 4.2 следует, что 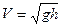есть максимальная скорость распространения поверхностных гравитационных волн (возмущений). Тогда при F_r<1 скорость потока V меньше, чем скорость распространения возмущений (удар о воду, волны от препятствия в потоке, превышение глубины от преграды и т.д.), равная 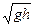, и возмущения в виде волны или системы волн распространяются против течения. При F_r>1,наоборот, возмущения, распространяясь со скоростью, меньшей, чем скорость потока V, не могут пройти выше того места, где возникли.

Задача 4.7. Жидкость плотности r находится в сообщающихся сосудахправильной формы. Каким-то образом ее вывели из положения равновесия, подняв уровень в правой части на величину x по отношению к левой (рис. 4.7), а затем предоставили самой себе. Жидкость в сосудах стала колебаться. Необходимо определить период колебаний столба жидкости в сосудах; трение не учитывать.

Решение.Процесс колебаний обусловлен переходом потенциальной энергии той части жидкости, которая превышает уровень в другой части, в кинетическую энергию всей жидкости (общей массы ее в обеих частях) - так как вся масса участвует в колебаниях - и обратно, в потенциальную энергию. Движущей силой в данном случае является сила тяжести, действующая на столб жидкости в правом сосуде высотой x.Заключаем потому, что в число основных параметров будут входить ускорение свободного падения g и общая длина всего столба жидкости в обеих частях l. Относительно величины x можно сделать вывод, что она должна Рис. 4.7

быть значительно меньше l, т.е. x<<l (рассматриваем задачи в линейном приближении). В данном случае прямая аналогия с малыми колебаниями маятника.

Элементарно получается такой результат

T=C

(комбинация в правой части единственная, имеющая размерность времени). Простота решения задачи в данном случае обусловлена симметрией обеих частей сообщающихся сосудов; оказывается, что период не должен зависеть ни от плотности жидкости, ни от сечения сосудов.

Задача 4.8. Методом анализа размерностей вывести зависимость для высоты подъема воды в открытой стеклянной трубке, опущенной в жидкость.

Решение. Из опытов известно, что чем меньше диаметр трубки, тем выше поднимается в ней жидкость, таким образом, одним из главных параметров в искомой зависимости является радиус трубки r. Поднятие жидкости происходит из-за сил поверхностного натяжения – поэтому коэффициент поверхностного натяжения жидкости 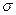также должен войти в зависимость. Поскольку на жидкость, кроме силы поверхностного натяжения действует сила тяжести и высота подъема зависит от веса столба жидкости, то в число аргументов необходимо добавить ускорение силы тяжести g. Предварительно, таким образом, установлен такой вид общей зависимости для высоты подъема жидкости

,

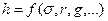в правую часть которой входит величина 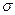, имеющая размерность 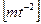и поэтому содержащая массу. Так как в левую часть масса не входит, то в аргументы правой части для исключения массы необходимо включить величину, содержащую массу; самым простым аргументом в данном случае является плотность 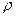. Такой путь рассуждений очевиден и часто применяется (особенно часто по отношению к массе).

Общая зависимость для h с учетом значения будет иметь вид

.

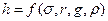Применяя затем стандартную систему решения к последней зависимости, получим

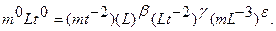
Система уравнений будет иметь вид

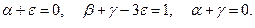
Имеем в данном случае три уравнения с четырьмя неизвестными; как и во многих подобных случаях, ищем наиболее простое решение. Из последней системы следует, что 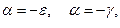поэтому 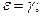из второго уравнения системы получаем 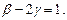Для простейшего решения положим 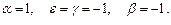Окончательно получаем

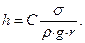
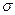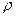Несколько иной путь решения состоит в том, что заранее можно сказать, как будут входить величины и в правую часть – в виде отношения 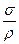(но не 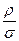) – чтобы масса сокращалась. С учетом данного замечания общий вид зависимости будет таким

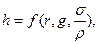
а после принятия стандартной схемы

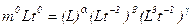
система уравнений будет иметь вид

.

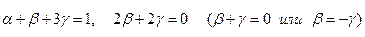Тогда из первого уравнения данной системы получается

.

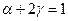Принимая в качестве простейшего решения 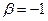, получим 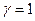, 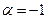и решение принимает вид

Если сформировать параметр, выражающий отношение силы поверхностного натяжения к силе тяжести, он будет иметь вид

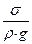
и размерность L² (безразмерный параметр в данном случае не имеет смысла – он будет просто числом и в систему уравнений не попадет). С учетом этого нового параметра зависимость для h будет иметь вид

Тогда имеем

,

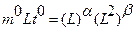откуда следует

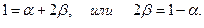
Принимая 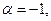получим 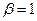и окончательно

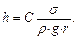
Задача 4.9.Найти выражение для силы, действующей на погруженное в жидкость твердое тело и направленной вверх (закон Архимеда).

Решение.Как всегда, на начальном этапе определим все величины, влияющие на искомую величину, в данном случае на силу. Прежде всего, представим себе, что в жидкость (например, в бак с водой) погружаются тела разного объема и при этом фиксируется сила, с которой они выталкиваются жидкостью. Легко представить себе, как будут различаться выталкивающие силы, действующие на футбольный мяч и мяч для игры в настольный теннис, если их поочередно погружать в воду. В результате делаем вывод, что сила зависит от объема тела.

На следующем этапе анализа представим небольшой шар, надутый водородом, который может подниматься вверх; если его попробовать погрузить в воду, то мы встретимся с силой, которая значительно превышает ту, которая существует в воздушной среде. Делаем вывод, что искомая сила зависит также от плотности среды, в которую погружено тело. Если представить на каком-нибудь простейшем примере (например, рассмотреть параллелепипед внутри жидкости), отчего возникает сила, то получим, что основной причиной является давление, существующее внутри жидкости, оно, в свою очередь, вызвано силой земного тяготения. Поэтому в число влияющих величин необходимо включить ускорение g. Несмотря на последнее замечание, попробуем не учитывать в искомой зависимости g; тогда

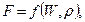
где W – объем тела,

и

.

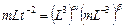Система уравнений имеет вид

.

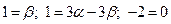В данном случае одно уравнение не имеет смысла ( 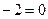) и вместо физического объема 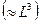будет входить объект размерности 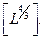С другой стороны, введение в правую часть сомножителя 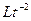(ускорения) делает все уравнения естественными, и поэтому заключаем, что искомая зависимость имеет вид

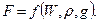
Тогда

,

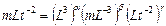и система уравнений имеет вид

.

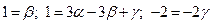Решение будет таким

.

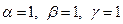Окончательно, искомая зависимость имеет вид

F=Wpg,

что полностью совпадает с аналитическим выражением закона Архимеда.

Задача 4.10. Установить вид зависимости для разности давлений (тяги), возникающей на входе в дымовую трубу.

Решение. Тяга (разность давлений) слева и справа от задвижки З у входа в трубу обусловлена разностью давлений , которую создают в своем основании столбы газа: атмосферного воздуха 1 и газообразных продуктов сгорания топлива 2. Если приближенно принять плотность газообразных продуктов внутри трубы постоянной по высоте и равной 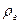, то тяга в конечном счете зависит от разности плотностей ;

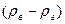при этом .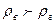

В башенных градирнях нагревается воздух и вместе с паром поднимается наверх. Размерность разности плотностей та же, что просто плотности. В число основных параметров зависимости для ∆p войдут также образцы: плотность ρ, ускорение свободного падения g, высота трубы H, так как вес столба зависит от g и H. Тогда

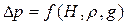
и применяя обычную схему решения, получим:

.

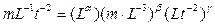Решая соответствующую систему уравнений, получим

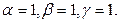
Окончательно выражение для 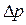имеет вид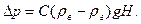

Относительное движение тела и жидкости

На практике встречается множество случаев взаимодействия жидкости и твердых тел - например, осаждение взвеси в отстойниках, движение корабля в воде, падение мельчайших капель жидкости в воздухе, полет самолета в атмосфере, воздействие водного потока на мостовую опору и т.д. Обычно в задачах об относительном движении тела и жидкости требуется определить:

а) силу, действующую на тело со стороны жидкости или газа;

б) скорость движения тела.

Основной задачей является все-таки определение зависимости для сил, действующих на тела, так как если они известны и равнодействующая их равна нулю, то движение равномерное. Это условие позволяет найти скорость движения тела, поэтому часто оказывается достаточным найти выражение для всех сил, действующих на тело. По этой причине ниже рассматриваются в основном примеры определения силы.

Выберем для тела некоторый линейный параметр l, скорость движения обозначим через V, а положение его определяется углом a. Привлекая опыт наблюдений над повседневными явлениями, заключаем, что при всех прочих равных условиях сила взаимодействия тем больше, чем больше площадь тела S в проекции на плоскость, перпендикулярную направлению скорости (площадь миделева сечения). Очевидно, что сила зависит и от скорости движения. При сравнении сил, действующих на тела в газах и жидкостях при одинаковых площадях и скоростях, заключаем, что плотность r также может влиять на силу. Получаем общую функциональную зависимость:

F=f(V,l,a,r,m),

(вид ее не изменится, рассматривается длина вектора силы или длина любой его проекции).

Пример 4.3.Найти вид зависимости для силы, действующей со стороны потока идеальной несжимаемой жидкости на тело.

Определяющими параметрами в данном случае являются следующие:

l,V ,r

(угол a, как безразмерную величину, не включаем в их число) и окончательно:

F=C(a)f(l,V,r).

Далее следует стандартный ход решения :

mLt^-2=L^a(Lt^-1)^b(mL^-3)^g,

система

g=1, b=2, a+b-3g=1,

ее решение

a=2, b=2, g=1.