Последнее равенство приводится к виду
t= La+g mb+g t-2g.
Решая систему, полученную в результате, найдем
a = 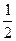 , b =
, b = 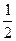 , g =
, g = 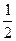 .
.
Для периода имеем
t =C 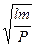 ,
,
и учитываем, что P=mg; тогда
t =C 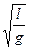 . (2.6)
. (2.6)
Видно, что решения, полученные двумя способами, совпадают. Если бы начальный угол был бы не 16°, а другой, то зависимость (2.6) была бы такой же, но постоянная C имела другое значение, поэтому в общем случае можно записать:
t=F(j) 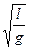 ,
,
где j – начальный угол отклонения маятника.
Вид функции F(j) из теории размерности определить нельзя. Если эту функцию разложить в ряд Тейлора и сохранить в ней только первый член (что можно делать в случае малых колебаний), то получим:
t=C 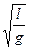 ,
,
где С – постоянный числовой коэффициент, значение которого из теории размерности определить также нельзя. Как известно, если j мало, то C » 2p. Ценным свойством метода анализа размерностей является то, что неизвестный постоянный коэффициент C, присутствующий во всех зависимостях в виде сомножителя, возможно определить, проделав один-единственный опыт. В данном случае достаточно взять нить длиной около двух метров и при известных величинах l и g определить с помощью секундомера период колебаний t. Затем величина C просто подсчитывается с помощью (2.6).
Замечание 2.4. Над размерными величинами правило размерности допускает выполнение только степенных математических операций. Все прочие операции (sin x, cos x, tg, ex, lnx и т.д.) могут выполняться тольконад безразмерными величинами. Правила размерности очень полезны для проверки формул. Если вычисления проводятся в какой-то одной системе единиц, то размерности обеих частей всех полученных равенств должны быть одинаковыми. Несовпадение размерностей указывает на присутствие ошибки, допущенной при вычислениях.
Пример 2.5.Получена зависимость для момента силы трения во вращающейся пяте, относительно оси вращения, в виде
M  К F(R2+r2),
К F(R2+r2),
где M – момент силы; F – сила трения; R и r – радиусы; К – безразмерный коэффициент трения. Проверить, нет ли ошибки в выражении для M.
Имеем следующие размерности величин[R]=[r]=L, [F]=Lmt-2, [M]=L2mt-2. Теперь видно, что размерности левой и правой частей зависимости для M не совпадают. Формула для M выведена неверно. Возможно рекомендовать заменить вторые степени R и r на первые.
Существует немало эмпирических зависимостей, полученных в результате обработки данных экспериментов. Они могут не удовлетворять правилу размерностей и поэтому верны в рамках строго определенных единиц.
Пример 2.6.Для кинематического коэффициента вязкости чистой пресной воды n существует формула, выражающая зависимость n от температуры
n = 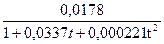 (см2/с),
(см2/с),
где t- температура в градусах по шкале Цельсия. В данном случае никакого соответствия размерностей правой и левой частей быть не может.
Пример 2.7.Для определения коэффициента C рекомендуется, в частности, использовать зависимость вида
C= 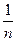 +17,72 lg R.
+17,72 lg R.
Коэффициент C входит в формулу для расхода Q=CS 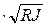 , где Q – расход; S – площадь; R – линейный параметр; J – безразмерный уклон. В данном случае имеем типичную эмпирическую зависимость для коэффициента C, в которой не только нарушено правило размерностей, но и под знаком логарифма находится размерная величина. Тем не менее зависимость для C успешно применяется для расчета открытых каналов.
, где Q – расход; S – площадь; R – линейный параметр; J – безразмерный уклон. В данном случае имеем типичную эмпирическую зависимость для коэффициента C, в которой не только нарушено правило размерностей, но и под знаком логарифма находится размерная величина. Тем не менее зависимость для C успешно применяется для расчета открытых каналов.
Рассмотрим еще один пример из механики.
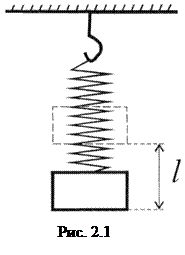
Пример 2.8.На упругой и закрепленной одним концом пружине подвешен груз массой m (рис.2.1). При удлинении пружины на длину l возникает упругая сила, равная по абсолютной величине f, которая стремится вернуть грузвисходное положение. Кроме силы f, на груз никакие другие силы не действуют. Определить время t возвращения груза в исходное положение.
Необходимо, таким образом, найти вид зависимости
t = j (l, m, f).
Относительно вида этой функции можно сделать следующие замечания.
 Если допустить, что в ее состав входят какие-либо тригонометрические, показательные или другие не алгебраические функции, то аргументами их могут быть только безразмерные величины. В системе единиц L, m, t из величин l, m и f, размерности которых равны соответственно L, m и Lmt-2, невозможно составить никакой безразмерной комбинации, так как t входит только в размерность силы. Поэтому в такую комбинацию, сила войти не может, а L и m не могут дать безразмерного сочетания. Таким образом, единственным возможным видом связи между t,l,m и f является
Если допустить, что в ее состав входят какие-либо тригонометрические, показательные или другие не алгебраические функции, то аргументами их могут быть только безразмерные величины. В системе единиц L, m, t из величин l, m и f, размерности которых равны соответственно L, m и Lmt-2, невозможно составить никакой безразмерной комбинации, так как t входит только в размерность силы. Поэтому в такую комбинацию, сила войти не может, а L и m не могут дать безразмерного сочетания. Таким образом, единственным возможным видом связи между t,l,m и f является
алгебраическая функция. Естественно искать эту функцию в виде
t=CLambf g. (2.7)
Переходя к размерностям
t=La mb (Lmt-2)g
или
L0 m0 t=La+g mb+g t-2g,
составляя систему уравнений для a, b и g, как в предыдущих примерах, и решая ее, получим
a= 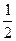 , b=
, b= 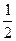 , g=-
, g=- 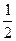 .
.
Окончательный ответ имеет вид
t=C  .
.
Если сила f пропорциональна l (как это имеет место при упругих силах), то обозначая f=Kl, можно представить время t в виде:
t=C 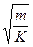 , (2.8)
, (2.8)
где K- коэффициент упругости пружины, так что время оказывается не зависящим от удлинения l (в действительности это верно только при малых значениях l). Точное решение задачи приводит к тому же уравнению (2.8), но с коэффициентом 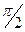 .
.
Задача 2.2.Определить вид зависимости для частоты колебаний струны от основных влияющих параметров (струна выполнена из металла плотности r и с некоторой силой натяжения зафиксирована между двумя точками).
Из приведенных примеров следует, что решение почти любой задачи методом анализа размерностей производится в два этапа:
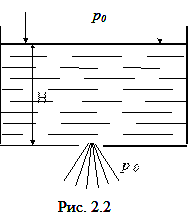 • на первом определяются и анализируются все входящие в искомую зависимость параметры и этот этап является решающим;
• на первом определяются и анализируются все входящие в искомую зависимость параметры и этот этап является решающим;
• на втором применяется формальный подход, редко встречающий затруднения.
Задача 2.3.Определить вид зависимости для скорости истечения жидкости в атмосферу через отверстие в дне открытого резервуара (рис. 2.2), глубина жидкости в котором равна H и поддерживается постоянной.
Решение.В процессе истечения потенциальная энергия положения жидкости переходит в кинетическую энергию вытекающей струи. Переход происходит согласно соотношению
 .
.
Рассмотрим возможные параметры, влияющие на скорость истечения. Напор H входит в выражение для потенциальной энергии и должен обязательно присутствовать. Так как истечение происходит благодаря силе тяжести, то необходимо учитывать в качестве одного из главных параметров ускорение силы тяжести g. Рассмотрим параметры: диаметр отверстия d, форма отверстия, толщина стенки, шероховатость стенок сосуда, степень приближения отверстия к стенкам, плотность жидкости ρ, вязкость ν.
В данном случае параметров больше трех и поэтому необходимо упростить рассмотрение процесса истечения для уменьшения их. Допустим прежде всего, что жидкость идеальная и исключим тем самым вязкость из рассмотрения. Далее предположим, что отверстие круглое и диаметр его значительно меньше H, допустим также, что толщина стенки не влияет, т.е. она тонкая. Зависимость для скорости принимает вид
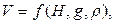
но по понятным причинам плотность, содержащая массу, в правую часть войти не может. Поэтому окончательно имеем
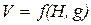 .
.
Применяя обычную схему решения, получаем:
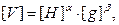 или
или 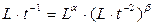 .
.
Для L имеем
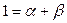 ,
,
аналогично для времени t:
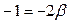 или
или 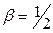 , поэтому
, поэтому 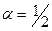 .
.
окончательно получаем для скорости:
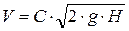 . (2.9)
. (2.9)
Зависимость для скорости, полученная иным способом, в действительности имеет вид:
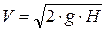 . (2.10)
. (2.10)
Если допустить, что жидкость реальная (вязкость её не равна нулю), то часть энергии переходит за счет трения в теплоту. Потенциальная энергия положения жидкости остается неизменной и за счет перехода части механической энергии в теплоту кинетическая энергия уменьшается по сравнению со случаем истечения идеальной жидкости. Если резервуар из предыдущей задачи сверху закрыт и в пространстве над жидкостью создано давление p1, больше атмосферного (рис.2.3), то появляется дополнительная сила, вызванная разностью давлений Dp=p1-p0 и заставляющая жидкость вытекать с большей скоростью. Для определения вида, зависимости типа (2.10), необходимо в число параметров включить Dp.Но в Dp входит масса, а в размерность левой части масса не входит, поэтому необходимо образовать параметр из Dp и такой величины, в которую бы входила масса, например плотности
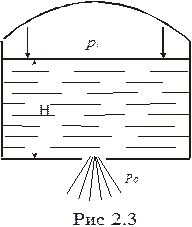
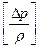 =
= 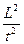 .
.
Можно предположить, что окончательный ответ в этом случае будет таким
V=C 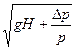 .
.
 Зависимость вида (2.10) может быть получена для самого общего случая в результате рассмотрения общих дифференциальных уравнений и, что самое главное, с учетом всех граничных условий, касающихся жидкости, формы и размеров резервуара и отверстия.
Зависимость вида (2.10) может быть получена для самого общего случая в результате рассмотрения общих дифференциальных уравнений и, что самое главное, с учетом всех граничных условий, касающихся жидкости, формы и размеров резервуара и отверстия.
Жидкость в действительности реальная и вязкость оказывает влияние на величину скорости. Можно также заранее допустить, что на величину скорости влияет форма резервуара, близость его стенок к отверстию, толщина стенки в отверстии, форма отверстия и его величина и т.д. Все эти факторы, если их включить (даже в виде безразмерных отношений) в общую функциональную зависимость V = f (H, g) не позволили бы применить метод анализа размерностей. Нами решена здесь задача при таких (заранее не известных и определенных) условиях, когда влиянием всех факторов, кроме H и g,можно пренебречь. Навыки применения метода анализа размерностей полезны, в частности, тем, что позволяют научиться выделять главные влияющие факторы.
 Пример 2.9.В цилиндрическом сосуде площадью сечения S1 налита жидкость до высоты H от дна. В дне сосуда выполнено отверстие площадью S2 (рис.2.4). Жидкость идеальная, плотность ее ρ. Определить время t полного опорожнения сосуда.
Пример 2.9.В цилиндрическом сосуде площадью сечения S1 налита жидкость до высоты H от дна. В дне сосуда выполнено отверстие площадью S2 (рис.2.4). Жидкость идеальная, плотность ее ρ. Определить время t полного опорожнения сосуда.
 По аналогии с предыдущими примерами необходимо допустить, что в число определяющих параметров должно входить ускорение свободного падения g. Действуя по известной схеме, представим истинное выражение для времени в виде
По аналогии с предыдущими примерами необходимо допустить, что в число определяющих параметров должно входить ускорение свободного падения g. Действуя по известной схеме, представим истинное выражение для времени в виде
t=CHagbrgS1dS2s,
или
L0m0t=La(Lt-2)b(mL-3)g(L2)d(L2)s. (2.11)
Приравнивая показатели степеней, левой и правой частей, получим систему уравнений
0=a+b-3g+2d+2s,
0=g, 1=-2b.
Показателей степени пять, а уравнения три. Два показателя определяем сразу: g=0, b=- 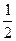 - это значит, что в данной схеме время истечения от плотности жидкости не зависит. Для определения остальных показателей степени требуется либо ввести дополнительные данные, либо сделать какие-то предположения. Например, если предположить, что скорость в отверстии не зависит от его площади, то время вытекания обратно пропорционально площади отверстия S2. При одинаковых начальных уровнях (при S2=const) время тем больше, чем больше S1. Поэтому можно предположить (но не доказать), что показатели d и s равны d=1, s =-1. Тогда сразу же определяется показатель a=
- это значит, что в данной схеме время истечения от плотности жидкости не зависит. Для определения остальных показателей степени требуется либо ввести дополнительные данные, либо сделать какие-то предположения. Например, если предположить, что скорость в отверстии не зависит от его площади, то время вытекания обратно пропорционально площади отверстия S2. При одинаковых начальных уровнях (при S2=const) время тем больше, чем больше S1. Поэтому можно предположить (но не доказать), что показатели d и s равны d=1, s =-1. Тогда сразу же определяется показатель a= 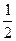 , и для времени вытекания имеем зависимость
, и для времени вытекания имеем зависимость
t=C 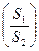
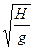 . (2.12)
. (2.12)
Определение показателя степени a возможно выполнить другим способом. Так как в задаче ничего не сказано о форме отверстия и форме сечения сосуда, то можно площадь отнести к числу основных единиц, не связывая ее с единицей длины. В этом случае вместо (2.11) время представится так
t=CLa(Lt-2)b(mL-3)g SdSs,
где S- условное обозначение размерности площади. Из этого уравнения дополнительно к условиям g=0, b=- 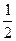 получим a=
получим a= 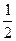 и d=-s. Поэтому решение задачи имеет вид
и d=-s. Поэтому решение задачи имеет вид
t=Cj 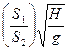 .
.
По сравнению с первоначальным решением, когда необходимы были дополнительные предположения, получилось более определенное решение благодаря введению дополнительной основной единицы.
Задача 2.4.Небольшая капля несжимаемой жидкости совершает пульсационные колебания, становясь последовательно вытянутой, сферической, сплюснутой, сферической, снова вытянутой и т.д. Как зависит период Т этих пульсаций от плотности ρ, поверхностного натяжения σ и радиуса капли r?
Решение.Представим каплю ртути на горизонтальном стекле; она имеет слегка сплюснутую форму, так как на ртуть действует сила тяжести. Если деформировать каплю и заставить ее колебаться, то необходимо учесть и действующую на нее силу тяжести, причем учет ее будет тем более необходим, чем больше размер капли. Если рассматривать очень малую каплю (~ 0,5 мм), то можно считать, что сила тяжести оказывает незначительное влияние. Причина этого состоит в том, что сила поверхностного натяжения пропорциональна площади поверхности (т.е. L2), а сила тяжести (вес) пропорциональна объему (т.е. L3). Для капель любых размеров условие задачи соответствует пространству внутри космического корабля на круговой орбите (т.е. в условиях невесомости).
Задача 2.5.Вывести формулу для давления в пузырьке воздуха, находящегося внутри жидкости с коэффициентом поверхностного натяжения σ.
Решение.Давление внутри пузырька будет обусловлено давлением в окружающем пространстве, и кроме того, теми силами поверхностного натяжения, которые стремятся сократить поверхность, ограничивающую пузырек. К примеру, в мыльном пузыре по этой причине давление больше, чем в окружающей его среде.
В данной задаче основным параметром, влияющим на давление, будет коэффициент поверхностного натяжения σ. Кроме этого параметра, очевиден еще только один – радиус пузырька r. Тогда зависимость от давления имеет вид
p = f (σ, r)
или, в терминах первичных параметров
mL-1t-1 = (mt-2)αLβ, α=1, β=-1
и искомая зависимость примет вид
p = C 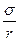 .
.
3.p-теорема и метод подобия
Приведенные примеры показывают, что анализ размерностей не может являться универсальным методом, позволяющим автоматически находить интересующие нас зависимости между физическими величинами. Применение анализа размерностей требует во многих случаях удачного выбора системы единиц, учета размерных постоянных.
Приведенные примеры показывают, кроме того, что чем меньше основных величин и чем больше параметров, участвующих в процессе (включая размерные, постоянные), тем более неполной является система уравнений, которую можно получить для нахождения показателей степени. В то же время возможны и такие случаи, когда уравнения размерностей приводят к несовместимой системе уравнений для показателей степеней в формулах размерностей. Это говорит о том, что какая-то из величин оказалась неучтенной.
Большую помощь при применении метода анализа размерностей оказывает так называемая p-теорема, которая может быть сформулирована так: уравнение, связывающее между собой n размерных величин, характеризующих изучаемое явление, может быть представлено в виде зависимости между n-k безразмерными комбинациями (комплексами) этих величин, где k- число основных единиц.
Допустим, что величина z является функцией n размерных величин
z=f(a1 ,a2 ,…,an). (3.1)
Можно доказать, что эта зависимость заменится уравнением
П=f(1,1,…,1,П1,П2,…,Пn-k), (3.2)
где П1,П2,…,Пn-k – безразмерные комплексы. Чем меньше разность n-k, тем определеннее будет решение задачи. При n-k=1 задача становится наиболее определенной и, как правило, однозначной. Выделяя из общего числа величин ту, зависимость которой от остальных мы хотим определить, возможно найти ее в виде явной функции.
Рассмотрим пример 2.8 с точки зрения p-теоремы. В этом примере четыре величины взаимосвязаны: масса груза, сила натяжения пружины, ее удлинение и время возвращения. Согласно p-теореме, при трех основных величинах- длине, массе и времени возможно из четырех величинобразовать одну безразмерную комбинацию. Соответственно связь между этими величинами можно записать в виде функции
j( f p lq mr tk)=const,
где аргумент функции( выражение в скобках) безразмерный и стоящая справа постоянная величина безразмерная. В аргументе функции, стоящей в левой части, все показатели степени возможно, сохраняя его безразмерным, изменить в одинаковое число раз, в результате чего один из показателей может быть сделан равным единице. Наиболее удобно это сделать для искомой величины, в данном случае для времени t
[f ahbmc t]=1.
Последнее уравнение равносильно уравнению (2.7) с той только разницей, что все показатели имеют обратные знаки.
Задача 3.1.Применяя p-теорему, получить выражение для безразмерного критерия, определяющего режим течения жидкости (критерия Рейнольдса). Из опыта известно, что в число определяющих величин входят: средняя скорость течения V, динамический коэффициент вязкости μ, плотность жидкости r, диаметр трубы d.
Решение. В данном случае показатель режима П- безразмерная величина
П=f(V,μ,ρ,d). (3.3)
Согласно p-теореме эту функцию можно выразить безразмерным комплексом из п-3=4-3=1, т.е. из одной величины
П=Vaµbrgdd, (3.4)
где a,b,g и d- неизвестные показатели.
Уравнение (3.4) представим как
L0m0t0=(Lt-1)a(mL-1t-1)b(mL-3)gLd
и получим систему a-b-3g+d=0, b+g=0, -a-b=0, из которой следует a=-b, a=g, a=d.
Искомый безразмерный комплекс приписывает вид
p= 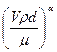 ,
,
где неизвестный показатель степени a может иметь любое значение, отличное от нуля, поскольку безразмерное число в любой степени останется безразмерным. Проще всего принять a=1; в этом случае
p=Re= 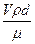 =
= 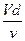 . (3.5)
. (3.5)
Выражение (3.5) представляет собой известный критерий, характеризующий режим движения жидкости; как известно, существует два режима- ламинарный и турбулентный, качественно отличные друг от друга. Принято считать, что если при течении жидкости с кинематическим коэффициентом вязкости v, со скоростью V в трубе диаметром d число Re<2300, то режим движения ламинарный, если Re>2300, то режим турбулентный.
Дата добавления: 2015-08-01; просмотров: 978;
