Окончательный ответ записывается так
S=Cat2. (2.2)
Искомая зависимость установлена нами с точностью до некоторого безразмерного постоянного множителя, определить который с помощью данного метода невозможно. Зависимость (2.2), полученная другим способом, в действительности имеет вид
S=at2/2,
т.е. C=1/2.
Замечание 2.1.В данном примере наблюдается очень типичный случай, когда с помощью метода анализа размерностей не удается точно определить значение постоянного безразмерного сомножителя. Его определить с помощью данного метода принципиально невозможно. Очень часто возможно измерить в опытах (или косвенно определить) все основные аргументы и искомую величину (они связаны соотношением, полученным методом анализа размерностей). Тогда становится возможным определить числовое значение ранее неизвестного коэффициента C, входящего в виде сомножителя. Часто для этого достаточно проделать всего лишь один опыт.
Замечание 2.2.С помощью метода анализа размерностей, как никаким другим методом, возможно быстро и просто получить зависимость, определяющую вид функции и порядок величин аргументов.
Замечание 2.3.В качествесомножителя, как это было в приведенном выше примере, в любую часть (2.1) возможно подставить любую величину в нулевой степени.
Задача 2.1.Определить вид зависимости для центростремительного ускорения при движении тела по окружности.
Указание. В число параметров, от которых зависит ускорение, входят радиус R и
скорость движения тела по окружности V.
Ответ: a= 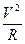 (здесь имеем тот случай, когда C=1).
(здесь имеем тот случай, когда C=1).
Пример 2.3.Найти вид зависимости для скорости свободного падения тела от высоты h, если начальная скорость равна нулю. В задаче рассматривается свободное падение тела, т.е. когда на него действует только сила тяжести. В действительности на тело действует сила сопротивления со стороны воздуха, но в данном случае она не учитывается.
Естественно, что скорость нарастает с расстоянием и поэтому основным аргументом в функциональной зависимости является расстояние от точки падения.
Так как падение происходит в поле силы тяжести, то в число исходных параметров должны входить высота h и ускорение g
V=f(g,h). (2.3)
Если включить в число аргументов (2.3) массу тела, то придется добавлять к ним плотность или силу, чтобы образовать параметры [m/ 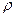 ]=L3, [F/m]=L/t2, в размерность которых масса не входит ( так как она не входит и в левую часть (2.3)). Размерности этих параметров уже входят в размерность правой части (2.3), так что делаем вывод, что в правую часть (2.3) масса не входит. Представляем правую часть (2.3) в степенном виде
]=L3, [F/m]=L/t2, в размерность которых масса не входит ( так как она не входит и в левую часть (2.3)). Размерности этих параметров уже входят в размерность правой части (2.3), так что делаем вывод, что в правую часть (2.3) масса не входит. Представляем правую часть (2.3) в степенном виде
V=Ch 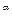 g
g 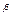 , (2.4)
, (2.4)
или, учитывая, что [V]=Lt –1, [g]=Lt –2, [h]=L, запишем (2.4) так
Lt –1=L 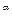 (Lt –2)
(Lt –2) 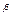 .
.
Для L равенство показателей степеней будет иметь вид: 1= 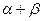 . Аналогично для t:
. Аналогично для t: 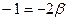 . Полученная система имеет решение
. Полученная система имеет решение 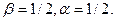 Окончательно зависимость (2.3) примет вид
Окончательно зависимость (2.3) примет вид
V=C 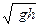 .
.
Пример 2.4.Математический маятник отклонен на угол 16° и отпущен без начальной скорости. Найти вид зависимости для периода колебаний маятника.
Математический маятник представляет собой тяжелую материальную точку, подвешенную на невесомой и нерастяжимой нити, которая закреплена другим своим концом неподвижно. Для наглядного представления процесса колебаний возможно его воспроизвести, привязав к тонкой прочной нити небольшой тяжелый груз и заставив его колебаться. Достаточно нескольких опытов с разными длинами нити, чтобы убедиться – на период колебаний влияет длина маятника (причем, чем короче нить, тем период меньше). Рассмотрим два способа решения, принципиально не отличающиеся друг от друга.
Способ 1. Колебания маятника представляют процесс перехода потенциальной энергии груза в кинетическую и обратно под действием силы тяжести; потенциальная энергия равна mgh и поэтому в число параметров должны входить ускорение свободного падения g и длина нити l. Для периода колебаний запишем
t=f(l,g)
или
t=La(Lt-2)b.
Решая полученную систему уравнений для значений a и b, получим a=0,5; b=-0,5. Окончательный результат имеет вид
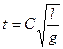 .
.
Способ 2.Будем считать в общем случае, что искомый период t зависит от длины маятника l, массы маятника m и его веса P.
Таким образом
t=f(l, m, P).
Дата добавления: 2015-08-01; просмотров: 710;
