Неравенство Бесселя

Левая часть в равенстве (1) неотрицательная, поэтому неотрицательной будет и правая часть:

,

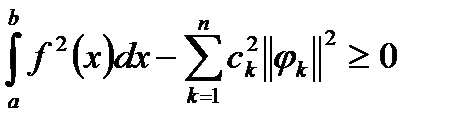Тогда

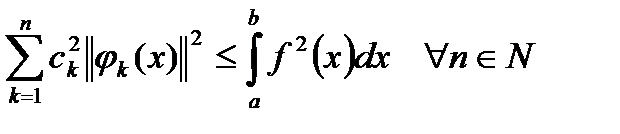. (2)

Левая часть последнего неравенства 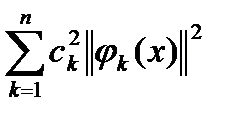- это n-ая усеченная сумма числового ряда 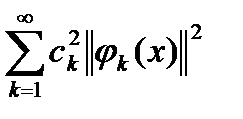с положительными членами. Неравенство (2) говорит об ограниченности сверху всей последовательности усеченных сумм ряда 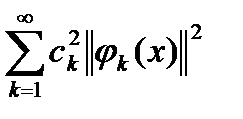, т.е. о его сходимости. Тогда если перейти к пределу в неравенстве (2) при 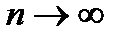, получим:

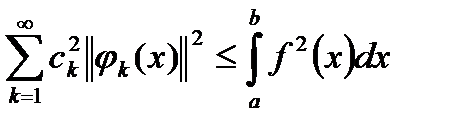
- неравенство Бесселя.

Вопросы

1. Определение квадратичного отклонения между функциями.

2. Свойства квадратичного отклонения между функциями.

3. Какая функция называется многочленом по ортогональной системе ?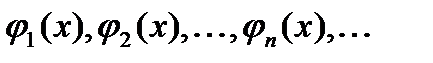

4. Сформулировать задачу о наименьшем квадратичном отклонении.

5. Какая функция называется многочленом Фурье по ортогональной системе ?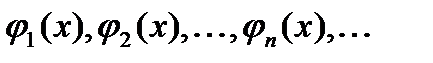

6. Вывести тождество Бесселя.

7.Вывести неравенство Бесселя.