Д.1. Коэффициент С как функция безразмерных переменных
Как следует из большинства рассматриваемых примеров и задач, постоянный множитель C представляет собой некоторую функцию безразмерных комплексов из величин, входящих в условие задачи.
Пример Д.1.1. Зависимость C от безразмерного параметра (угла j) встречается в примере 2.4 при определении периода колебаний математического маятника
T= F(j)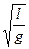 
.
Вид функции F(j) методом анализа размерности определить не удается; если эту функцию разложить в ряд Тейлора и сохранить только первый член, то получим, что F(j)=C. Такое разложение можно выполнить при любом значении угла, но для простоты (и это очень часто оправдывается) разложение можно производить для малых значений аргументов (вблизи нуля). В данном случае значение C методом анализа размерности оценить нельзя, но другими способами определено, что C=2p. Окончательно
T=2p 
.
Пример Д.1.2. Время истечения жидкости из сосуда, как следует из примера 2.9, равно
t=Cj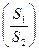 
.
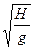Здесь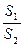 
>>1 и аргумент не является малым. Правильный результат для времени получается, если отождествить аргумент и функцию, т.е.
t=C .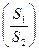
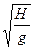Необходимость разложения в ряд и результат, следующий из этого, не исследованы.
Пример Д.1.3.Для расхода жидкости, протекающей через водослив в примере 4.1 получено выражение
Q=Cl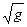 
H 
.
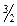Логично было бы составить малый параметр из аргументов, входящих в условие задачи, и разложить C по этому параметру в ряд.
Пример Д.1.4.В задаче 4.2 получена зависимость для давления в критической точке цилиндра, обтекаемого потоками идеальной жидкости
p=Cr V2.
Очевидно, что давление при переходе от критической точки к любой ближайшей изменится. Поэтому в полученной зависимости безразмерный параметр C может оказаться функцией расстояния r от центра цилиндра - функции безразмерного отношения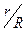 
, где R- радиус цилиндра.
Пример Д.1.5.если в задаче 4.7 представить, что стенки обеих частей сообщающихся сосудов (правой и левой) строго вертикальны, то можно предположить (если S1≠S2), что постоянная C будет зависеть от отношения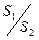 
(S2>S1), где S1 – например, площадь трубки в левой части,
S2 – площадь трубки в правой части.
Пример Д.1.6.В примере 4.3 в выражении для силы присутствует сомножитель C(a), где a – некоторый угол, определяющий положение тела. При малых углах эта функция может быть разложена в ряд Маклорена
Если условие задачи позволяет допустить, что С(0)=0, то получаем для C(a) приближение в виде (учитываем только первые два члена разложения)
C(a)=aC,
что иногда упрощает поиск зависимости C(a) в опытах.
Замечание Д.1. Если в левую часть функциональной зависимости не входит масса (например, выражения для скорости, расстояния и т.д.), а в правую входят величины, содержащие ее, то можно предположить, в каком виде эти величины включены в правую часть. Например (см. задачу 4.4), очевидно, что скорость звука в твердой среде зависит от упругих свойств этой среды – от модуля упругости E: [E] = mL-1t-1. Ясно, что в число аргументов должна войти плотность и параметр в правой части запишется в виде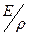 
. Аналогичными примерами сказанного служат задачи 4.2, 4.5.
Замечание Д.2.Обычно основные трудности в методе анализа размерностей встречаются при рассмотрении физического смысла явления и при выборе основных аргументов, от которых зависит искомая величина. Рассмотрим трудности другого типа, которые встречаются при применении так называемой стандартной схемы, причем часто, как и при анализе физического смысла, заранее невозможно дать каких-либо гарантированных рецептов или рекомендаций.
При решении гидравлических задач первичными (основными) величинами являются масса m, длина l и время t. Именно по степеням этих трех величин составляется система уравнений и поэтому уравнений в этой системе не может быть больше трех. Аргументов, от которых зависит искомая величина, может быть значительно больше и поэтому неизвестных в системе уравнений может быть больше, чем самих уравнений. Система, таким образом, будет неопределенной. К анализу этой системы нельзя подходить формально и приходится привлекать представления о физическом смысле рассматриваемого явления. Приведем пример изложенных замечаний.
В задаче 4.3 определяется скорость стекания пленки жидкости по вертикальной стенке без учета поверхностного натяжения. Общее выражение для скорости будет иметь вид
V = f (x,g,ν).
В дальнейшем (см. задачу 4.3) получаются два уравнения (так как масса не входит ни в левую, ни в правую части) с тремя неизвестными
α + β + 2γ = 1, γ + 2 β = 1.
Удачным выбором в данном случае следует считать β=1. Имея в виду, что скорость обратно пропорциональна вязкости, также логично можно было бы вначале выбрать γ = -1.
Во многих случаях можно уменьшить число аргументов, образовав из них отношения и эти отношения считать новыми аргументами – тем самым уменьшив число неизвестных и сделав систему определенной. Например, в рассматриваемом примере ясно, что стекание пленки происходит под действием силы тяжести. Силы вязкости, напротив, тормозят движение. Поэтому возможно образовать параметр, определяющий соотношение этих противоположно направленных сил; этот параметр будет иметь вид
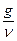и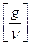 
= L-1t-1.
Дата добавления: 2015-08-01; просмотров: 695;