Понятие обобщенной функции. Дельта-функция Дирака. Интегральное каноническое представление случайных процессов.
Обобщенной функцией называется предел последовательности однопараметрического семейства непрерывных функций.
Дельта-функция Дирака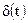 
- это обобщенная функция, являющаяся результатом предельного перехода при 
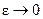в семействе функций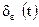 
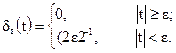
Среди свойств 
-функции отметим следующее:
1. 
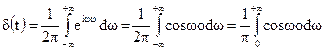
2. 
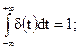
3. Если f(t)- непрерывная функция, то
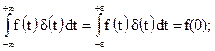
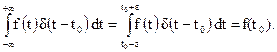
Случайный процесс Х(t), корреляционная функция которого имеет вид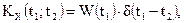 
называется нестационарным «белым шумом». Если W(t1)=W - const, то Х(t)-стационарный «белый шум».
Как следует из определения, никакие два, даже сколь угодные близкие, сечения «белого шума» не коррелированны. Выражение W(t) называется интенсивностью «белого шума».
Интегральным каноническим представлением случайного процесса Х(t) называется выражение вида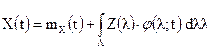 
где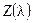 
- случайная центрированная функция; 
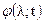- неслучайная функция непрерывных аргументов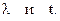 
Корреляционная функция такого случайного процесса имеет вид:
.
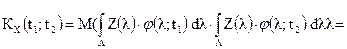
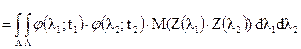Можно показать, что существует неслучайная функция G(λ) такая, что
где G(λ1) - плотность дисперсии; δ(х) - дельта-функция Дирака. Получаем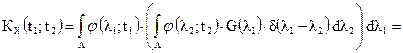 
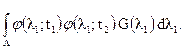
Следовательно, дисперсия случайного процесса Х(t):
.
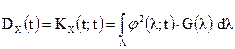Дата добавления: 2015-07-30; просмотров: 1072;