Достаточные условия эргодичности
Теорема 1. Стационарный случайный процесс X(t) эргодичен относительно
математического ожидания, если его корреляционная функция
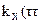 стремится к нулю при τ→∞;
стремится к нулю при τ→∞;
при этом: 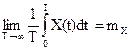 .
.
Теорема 2. Стационарный случайный процесс X(t) эргодичен относительно
дисперсии, если корреляционная функция стационарного слу-
чайного процесса Y(t)=X2(t) стремится к нулю при τ→∞;
при этом: 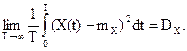
Теорема 3. Стационарный случайный процесс X(t) эргодичен относительно
корреляционной функции, если стремится к нулю при τ→∞ кор-
реляционная функция стационарного случайного процесса
Z(t, τ)= 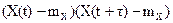 ;
;
при этом: 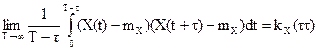
При практических расчетах интервал (0;Т) разбивается на n равных частей 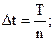 в каждом промежутке выбирается точка ti(например, середина). Если ограничиться формулой прямоугольников, получаем
в каждом промежутке выбирается точка ti(например, середина). Если ограничиться формулой прямоугольников, получаем
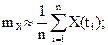
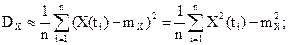
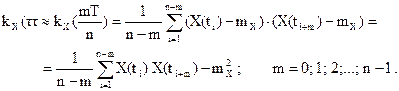
Дата добавления: 2015-07-30; просмотров: 1057;
