Стационарно связанные случайные процессы. Производная и интеграл от стационарного случайного процесса
Cлучайные процессы X(t) и Y(t) называются стационарно связанными, если их взаимная корреляционная функция зависит только от разности аргументов τ =t2-t1:  RXY(t1;t2)=rXY(τ).
RXY(t1;t2)=rXY(τ).
Стационарность самих случайных процессов X(t) и Y(t) не означает их стационарной связанности.
Отметим основные свойства стационарно связанных случайных процессов, производной и интеграла от стационарных случайных процессов,
1) rXY(τ)=rYX(-τ).
2) 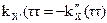
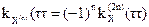
3) 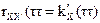

4) 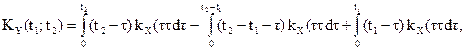
где 
5) 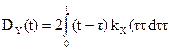 где
где 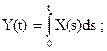
6) 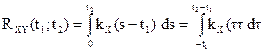 ;
;
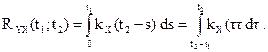
Дата добавления: 2015-07-30; просмотров: 1854;
