Линейные и нелинейные преобразования случайных процессов
Рассматривается следующая задача: на вход системы (устройства, преобразователя) S подается «входной сигнал», имеющий характер случайного процесса Х(t). Система преобразовывает его в «выходной сигнал» Y(t):
.
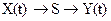Формально преобразование случайного процесса Х(t) в Y(t) может быть описано с помощью так называемого оператора системы Аt:
Y(t)=At(Х(t)).
Индекс t показывает, что данный оператор осуществляет преобразование по времени. Возможны следующие постановки задачи о преобразовании случайного процесса.
1. Известны законы распределения или общие характеристики случайного процесса Х(t) на входе в систему S, задан оператор Аt системы S, требуется определить закон распределения или общие характеристики случайного процесса Y(t) на выходе системы S.
2. Известны законы распределения (общие характеристики) случайного процесса Х(t) и требования к случайному процессу Y(t); надо определить вид оператора Аt системы S, наилучшим образом удовлетворяющего заданным требованиям к Y(t).
3. Известны законы распределения (общие характеристики) случайного процесса Y(t) и задан оператор Аt системы S; требуется определить законы распределения или общие характеристики случайного процесса Х(t).
Принята следующая классификация операторов Аt системы S:
Операторы системы
Линейные L Нелинейные N
Линейные однородные L0 Линейные неоднородные Lн
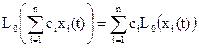
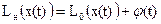
1. Рассмотрим воздействие линейной неоднородной системы
Lн(...)=L0(…)+φ(t)
на случайный процесс Х(t), имеющий следующее каноническое разложение:
.
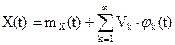Получаем:
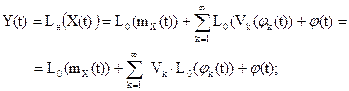
введем обозначения
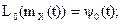
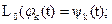
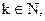
тогда каноническое разложение Y(t) приобретает вид:
.
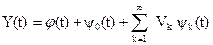Математическое ожидание случайного процессаY(t):
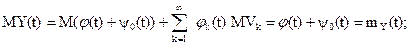
корреляционная функция случайного процесса Y(t):
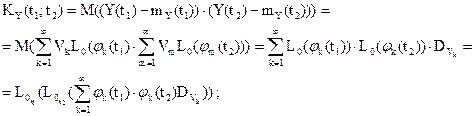
следовательно,
.
С другой стороны
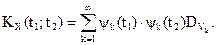
Дисперсия случайного процесса Y(t):
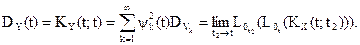
В заключении этого пункта отметим, что операторы дифференцирования и интегрирования случайных процессов являются линейными однородными.
2. Рассматривается квадратичное преобразование:
Y(t)=(X(t))2,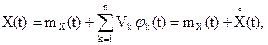 
Vk-центрированные случайные величины, имеющие симметричное относительно нуля распределение; любые четыре из них независимы в совокупности. Тогда
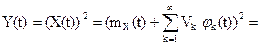
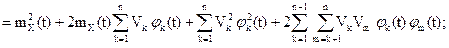
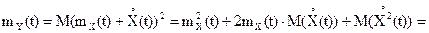
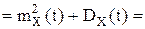
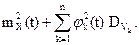
Введем неслучайные функции
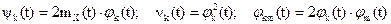
и случайные величины
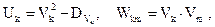
тогда случайный процесс Y(t) приобретает вид
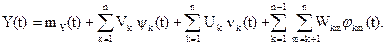
Получено каноническое разложение случайного процесса Y(t). Корреляционная функция Y(t):
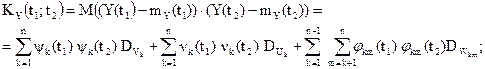
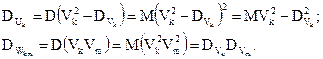
Дисперсия: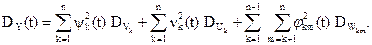 
Дата добавления: 2015-07-30; просмотров: 2510;