Понятие канонического разложения случайного процесса

Случайная величина V называется центрированной, если ее математическое ожидание равно 0. Элементарным центрированным случайным процессом называется произведение центрированной случайной величины V на неслучайную функцию φ(t): X(t)=V φ(t). Элементарный центрированный случайный процесс имеет следующие характеристики:

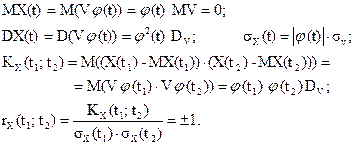
Выражение вида 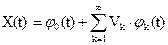, где φ_k(t), k=1;2;…-неслучайные функции; 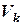, k=1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X(t), при этом случайные величины 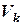называются коэффициентами канонического разложения; а неслучайные функции φ_k(t) - координатными функциями канонического разложения.

Рассмотрим характеристики случайного процесса

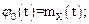
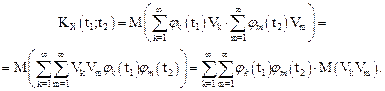
Так как по условию 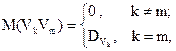то

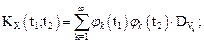
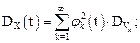
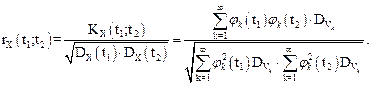
Очевидно, что один и тот же случайный процесс имеет различные виды канонического разложения в зависимости от выбора координатных функций. Более того, даже при состоявшемся выборе координатных функций существует произвол в распределении случайных величин V_к. На практике по итогам экспериментов получают оценки для математического ожидания и корреляционной функции: 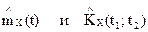. После разложения 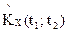в двойной ряд Фурье по координатным функциям φ_к(t):

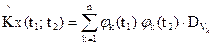
получают значения дисперсий 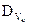случайных величин V_k.