Интеграл от случайного процесса и его свойства
Интегралом от случайного процесса X(t) на отрезке [0, t] называется предел в среднеквадратичном при λ→0 (n→0)
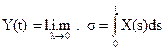
интегральных сумм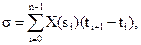 
где si 
(ti; ti+1); λ=max(ti+1 - ti), i=0,…,n-1.
Теорема 4. Математическое ожидание интеграла от случайного процесса равно интегралу от его математического ожидания: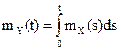 
, 
.
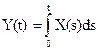Теорема 5. Корреляционная функция интеграла от случайного процесса X(t) равна двойному интегралу от его корреляционной функции: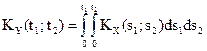 
.
Теорема 6. Взаимная корреляционная функция случайного процесса X(t) и его интеграла равна интегралу от корреляционной функции случайного процесса X(t):
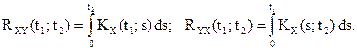
Дата добавления: 2015-07-30; просмотров: 2130;