Производная случайного процесса и ее свойства
В соответствии с классическим определением, производная случайного процесса X(t) должна быть определена как предел разностного отношения 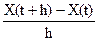 при h→0 в смысле соответствующей сходимости. Можно показать, что сходимость по вероятности обладает рядом недостатков, которые делают этот подход практически бесполезным.
при h→0 в смысле соответствующей сходимости. Можно показать, что сходимость по вероятности обладает рядом недостатков, которые делают этот подход практически бесполезным.
Случайный процесс X(t) называется дифференцируемым, если существует случайный процесс 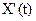 такой, что
такой, что 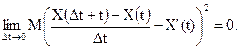
При этом случайный процесс 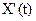 называется производной случайного процесса X(t) и обозначается следующим образом:
называется производной случайного процесса X(t) и обозначается следующим образом: 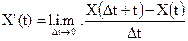 .
.
Теорема 1. Математическое ожидание производной случайного процесса равно производной от математического ожидания самого случайного процесса: 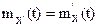 .
.
Следствие. 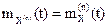 .
.
Теорема 2. Корреляционная функция производной случайного процесса X(t) равна второй смешанной производной от его корреляционной функции:  .
.
Теорема 3. Взаимная корреляционная функция случайного процесса X(t) и
его производной 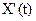 равна частной производной его корреляционной функции по переменной, соответствующей производной:
равна частной производной его корреляционной функции по переменной, соответствующей производной: 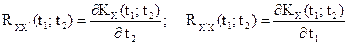 .
.
Дата добавления: 2015-07-30; просмотров: 2738;
