Классические виды сходимости

В стандартном курсе математического анализа вводятся следующие типы сходимости.

а) Числовая последовательность {x_n} называется сходящейся к числу х при n®¥, если для любого e>0 (сколь угодно малого) существует номер N_e, начиная с которого все последующие элементы последовательности принадлежат e-окрестности точки х:

;

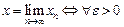
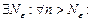
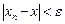б) Функциональная последовательность {f _n(x)} называется поточечно сходящейся на множестве Х к функции f (x), если она сходится (как числовая последовательность) при каждом фиксированном хÎХ к значению f (x).

Частным случаем поточечной сходимости является равномерная сходимость.

в) Функциональная последовательность {f _n(x)} называется сходящейся почти всюду на множестве Х к функции f (x), если она сходится поточечно к f (x) на множестве Х за исключением множества точек Х₀ меры нуль.

В теории вероятности такое понимание сходимости (кроме в)) мало содержательно. Тем не менее, приведенные здесь определения позволяют в полной мере ощутить разницу классических подходов и их вероятностных аналогов.