Корреляционная функция случайного процесса и ее свойства. Нормированная корреляционная функция

Корреляционной функцией случайного процесса X(t) называется неслучайная функция K_X(t₁; t₂) двух независимых аргументов, значение которой равно корреляционному моменту сечений, соответствующих моментам времени t₁ и t₂:

K_X(t₁; t₂)=M((X(t₁)-m_X(t₁))×(X(t₂)-m_X(t₂))).

Основные свойства корреляционной функции:

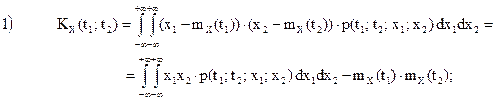
2) K_X(t; t)=D_X(t);

3) K_X(t₁; t₂)= K_X(t₂; t₁);

4) если φ(t) - неслучайная функция, то

K_φ(t)(t₁; t₂)=0; K_φ(t)+X(t)(t₁; t₂)= K_X(t)(t₁; t₂);

K_φ(t)×X(t)(t₁; t₂)= φ(t₁)× φ(t₂)×K_X(t)(t₁; t₂);

5)

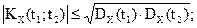
6)

Функция вида 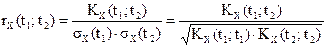называется нормированной корреляционной функцией.