Сходимость по вероятности
Говорят, что последовательность случайных величин {Хn} сходится по вероятности к случайной величине Х при n®¥, если
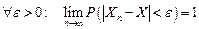 .
.
Обозначение: 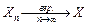
Обратите внимание, что при n®¥ имеет место классическая сходимость вероятности 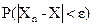 к 1, то есть с возрастанием номера n можно гарантировать сколь угодно близкие к 1 значения вероятности. Но при этом нельзя гарантировать близости значений случайных величин Хn к значениям случайной величины Х ни при каких сколь угодно больших значениях n, поскольку мы имеем дело со случайными величинами.
к 1, то есть с возрастанием номера n можно гарантировать сколь угодно близкие к 1 значения вероятности. Но при этом нельзя гарантировать близости значений случайных величин Хn к значениям случайной величины Х ни при каких сколь угодно больших значениях n, поскольку мы имеем дело со случайными величинами.
Случайный процесс X(t), tÎT называется стохастически непрерывным в точке t0ÎT, если 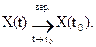
3. Сходимость в среднем в степени p³1
Говорят, что последовательность случайных величин {Xn} сходится в среднем в степени p³1 к случайной величине Х, если
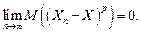
Обозначение: Xn 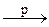 X.
X.
В частности, {Xn} сходится в среднеквадратичном к случайной величине Х, если
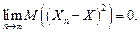
Обозначение: 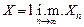 или
или 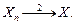
Случайный процесс X(t), tÎT называется непрерывным в среднеквадратичном в точке t0ÎT, если 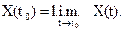
Дата добавления: 2015-07-30; просмотров: 1333;
