Математическое ожидание и дисперсия случайного процесса. Среднеквадратическое отклонение
Если в каждом сечении случайного процесса существует математическое ожидание, то математическим ожиданием случайного процесса X(t) называется неслучайная функция mX(t), значение которой при каждом фиксированном значении t равно математическому ожиданию соответствующего сечения:
mX(t)=MX(t).
Основные свойства математического ожидания случайного процесса: если φ(t) - неслучайная функция, то
М φ(t)=φ(t); М(φ(t)×X(t))=φ(t)×mX(t);
M(X1(t)+X2(t))=  ; M(X(t)+φ( t))= mX(t)+ φ(t).
; M(X(t)+φ( t))= mX(t)+ φ(t).
Если в каждом сечении случайного процесса существует дисперсия, то дисперсией случайного процесса X(t) называется неслучайная функция DХ(t), значение которой при каждом фиксированном значении аргумента t равно дисперсии соответствующего сечения:
DX(t)= DХ(t)= M(X(t)-mX( t))2.
Основные свойства дисперсии случайного процесса:
если φ(t) - неслучайная функция, то
D(φ(t))=0; D(φ(t)×X(t))=φ2(t)×DX(t);
D(X(t)+φ(t))=DX(t); 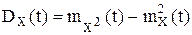 .
.
Среднеквадратическим отклонением случайного процесса X(t) называется арифметический квадратный корень из его дисперсии:
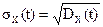 .
.
Дата добавления: 2015-07-30; просмотров: 1211;
