Определение случайного процесса. Основные подходы к заданию случайных процессов. Понятие реализации и сечения. Элементарные случайные процессы.

Случайным (стохастическим, вероятностным) процессом называется функция действительного переменного t, значениями которой являются соответствующие случайные величины X(t).

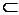В теории случайных процессов t трактуется как время, принимающее значения из некоторого подмножества Т множества действительных чисел (t T, T R).

В рамках классического математического анализа под функцией y=f(t) понимается такой тип зависимости переменных величин t и y, когда конкретному числовому значению аргумента t соответствует и притом единственное числовое значение функции y. Для случайных процессов ситуация принципиально иная: задание конкретного аргумента t приводит к появлению случайной величины X(t) с известным законом распределения (если это дискретная случайная величина) или с заданной плотностью распределения (если это непрерывная случайная величина). Другими словами, исследуемая характеристика в каждый момент времени носит случайный характер с неслучайным распределением.

Значения, которые принимает обычная функция y=f(t) в каждый момент времени, полностью определяет структуру и свойства этой функции. Для случайных процессов дело обстоит иным образом: здесь совершенно не достаточно знать распределение случайной величины X(t) при каждом значении t, необходима информация об ожидаемых изменениях и их вероятностях, то есть информация о степени зависимости предстоящего значения случайного процесса от его предыстории.

Наиболее общий подход в описании случайных процессов состоит в задании всех его многомерных распределений, когда определена вероятность одновременного выполнения следующих событий:

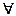t₁, t₂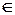,…,t_n T, n 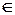N: X(t_i)≤x_i; i=1,2,…,n;

F(t₁;t₂;…;t_n;x₁;x₂;…;x_n)=P(X(t₁)≤x₁; X(t₂)≤x₂;…; X(t_n)≤x_n).

Такой способ описания случайных процессов универсален, но весьма громоздок. Для получения существенных результатов выделяют наиболее важные частные случаи, допускающие применение более совершенного аналитического аппарата. В частности, удобно рассматривать случайный процессX(t, ω) как функцию двух переменных: t 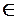T, ω 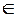Ω, которая при любом фиксированном значении t 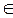T становится случайной величиной, определенной на вероятностном пространстве (Ω, A, P), где Ω - непустое множество элементарных событий ω; A - σ-алгебра подмножеств множества Ω, то есть множество событий; P - вероятностная мера, определенная на A.

Неслучайная числовая функция x(t)=X(t, ω₀) называется реализацией (траекторией) случайного процесса X(t, ω).

Сечением случайного процесса X(t, ω) называется случайная величина, которая соответствует значению t=t₀.

Если аргумент t принимает все действительные значения или все значения из некоторого интервала T действительной оси, то говорят о случайном процессе с непрерывным временем. Если t принимает только фиксированные значения, то говорят о случайном процессе с дискретным временем.

Если сечение случайного процесса - дискретная случайная величина, то такой процесс называется процессом с дискретными состояниями. Если же любое сечение - непрерывная случайная величина, то случайный процесс называется процессом с непрерывными состояниями.

В общем случае задать случайный процесс аналитически невозможно. Исключение составляют так называемые элементарные случайные процессы, вид которых известен, а случайные величины входят как параметры:

X(t)=Х(t,A₁,…,A_n), где A_i, i=1,…,n - произвольные случайные величины с конкретным распределением.