Потоки событий.

Поток событий – последовательность событий, которые наступают в случайные моменты времени.

Свойства потоков:

1. Стационарность потока.

Поток называется стационарным, если вероятность появления ровно m- событий на промежутке времени длительностью зависит только m и , и не зависит от момента времени, в который этот временной промежуток начался.

2. Отсутствие последствия.

Говорят, что поток обладает свойством отсутствия последствия, если вероятность появления m- событий на любом промежутке времени не зависит от того, появились или нет события в момент времени непосредственно предшествующий началу рассматриваемого промежутка.

Предыстория потока не сказывается на вероятности появления событий в будущем.

Если поток обладает таким свойством, то выполняется взаимная независимость числа событий в непересекающихся промежутках времени.

3. Ординарность потока.

Говорят, что поток обладает свойством ординарности, если за бесконечно малые промежутки времени может произойти не более одного события в потоке, т.е. появление 2-х и более событий практически невозможно.

4. Простейший (Пуассоновский) поток.

Простейшим потоком называется поток, который обладает всеми тремя свойствами.

Теорема: Если поток представляет собой сумму большого числа независимых стационарных потоков, влияние каждого на сумму ничтожно мало, то ординарный поток при условии его ординарности является простейшим.

Определение: Интенсивность потока называется среднее число событий происходящих за единицу времени.

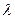- интенсивность

m – событий за промежуток времени

; ;

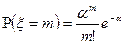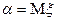Замена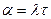

Простейший поток должен обладать 3-мя свойствами:

1. Стационарность.
2. Отсутствие последствия.
3. Ординарность.

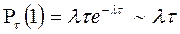
Пример: На телефонную станцию поступают 2 вызова в 1 минуту. Какова вероятность, что за 5 минут наступит 12 звонков.

Дано:

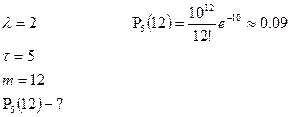
Введение в теорию цепей Маркова.

Цепь Маркова – последовательность испытаний, в каждом из которых, появляется и при том только один из несовместных событий 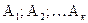. При этом условная вероятность 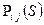того, что в испытании с номером S наступит событие 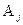при условии, что в S-1 испытании было 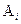не зависит от результатов предшествующих испытаний.

События 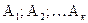называются состояниями системы, а сами испытания называются изменениями состояний системы.

Если изменение состояний происходит в фиксированные моменты времени, то такая цепь называется цепью Маркова с дискретными временами.

Если изменение состояний происходит в произвольные моменты времени, то цепь Маркова называют цепью с непрерывным временем.

Цепь Маркова называется однородной, если условная вероятность 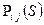перехода из состояния 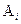в состояние 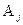не зависит от номера испытания S.

№1 №2 №3 №S-1 №S №S+1

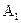
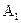
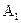
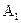
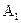
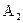
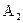
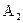
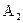
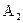
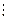
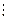
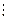
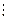
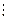
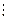
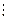
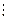
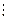
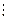
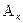
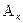
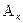
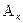
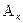
Для однородных цепей Маркова 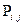называются переходными вероятностями.

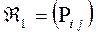
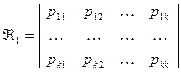
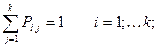
Равенство Маркова.

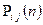- вероятность перехода из состояния 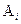в 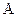; за n испытаний.

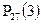
m n-m

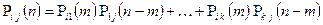
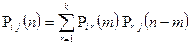
1) n = 2; m=1;

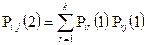
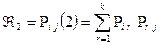
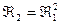
2) n = 3; m = 1;

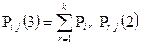
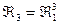
3)

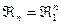
Пример:

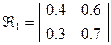
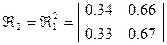
Производные функции.

Определение: Дискретная случайная величина 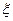называется целочисленной, если она принимает только целые неотрицательные значения 0; 1; 2; 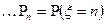с соответствующими вероятностями.

Определение: Производящей функцией целочисленной случайной величины 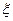называется функция вида: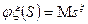

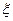
	0	1

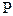
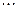
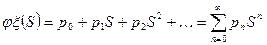
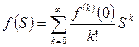- разложение функции в ряд Макларена

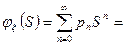
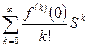
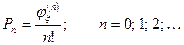
1. Биноминальное распределение.

Количество испытаний n с вероятностью успеха p, неуспеха q.

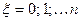
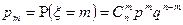
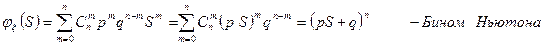
2. Распределение Пуассона.

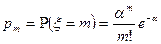
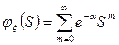
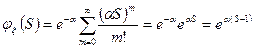
3. Геометрическое распределение.

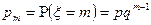
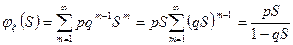
Факториальным моментом порядка к случайной величины 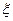называется:

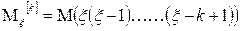
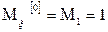
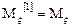
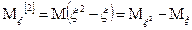
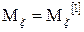
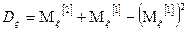
Теорема:

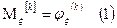
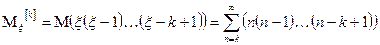
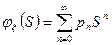
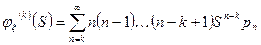
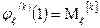
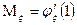
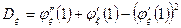
1. Биноминальное распределение.

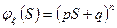
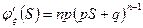
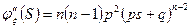
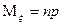
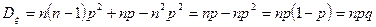
2. Распределение Пуассона.

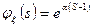
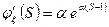
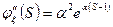
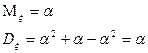
3. Геометрическое распределение.

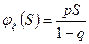
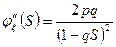
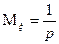
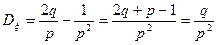
Теорема о мультипликативном свойстве производящих функций.

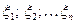- независимые целочисленные случайные величины, имеющие производящие функции 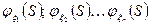, то

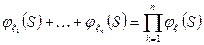
Доказательство:

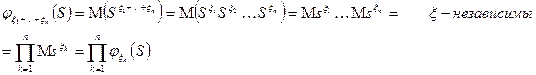
Пример: 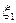- биноминальное распределение случайной величины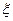

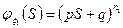
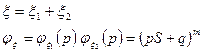
Характеристические функции.

Пусть 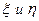действительные случайные величины с конечными 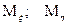, тогда случайная величина 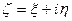называется комплексной случайной величиной, имеющей математическое ожидание .

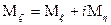Все основные свойства математических ожиданий переносятся и на случай комплексных случайных величин.

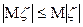
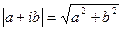
Определение: Характеристической функцией случайной величины 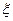называется функция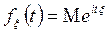

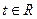
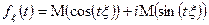
Если известна функция распределения 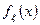или 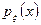, то явная запись будет

В случае дискретных случайных величин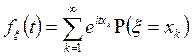

Свойства характеристической функции:

1)

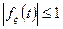
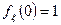
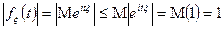
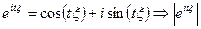
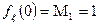
2) Характеристическая функция равномерно непрерывна по аргументу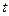

3) Если случайные величины 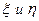связаны минимальным соотношением ,

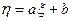где 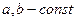, то

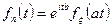
Доказательство:

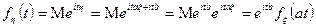
4)

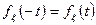
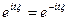
5) Мультипликативное свойство характеристической функции.

Если случайные величины 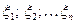- независимы, то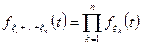

Доказательство:

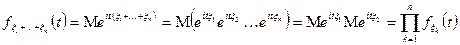
6) Пусть 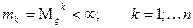, тогда характеристическая функция дифференцируема до порядка n включительно, выполняется следующее соотношение

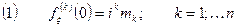
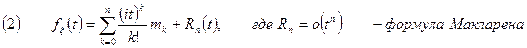
Доказательство:

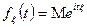
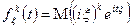
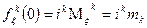
7)Если 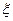дискретная целочисленная случайная величина, то ее характеристическая и производящая функции связанны следующей формулой:

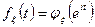
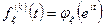
Примеры характеристических функций.

1. Биноминальное распределение. n – экспериментов, р – вероятность успеха.

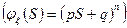
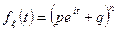
2. Распределение Пуассона.

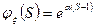
3. Геометрическое распределение.

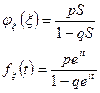
4.

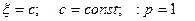
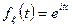
5. Нормальное распределение.

а) Нормальное распределение (0; 1)

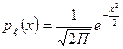
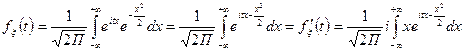
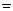
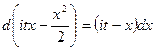
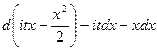
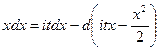
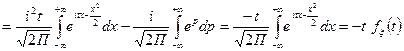
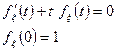
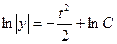
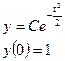
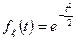
б) Произвольное нормальное распределение

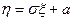, если 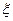- нормально распределенная случайная величина с параметрами (0;1),

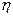- нормально распределенная случайная величина с параметрами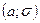

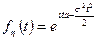
Замечание о сумме нормальных распределений:

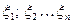
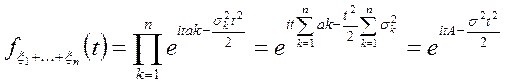
Сумма нормальных распределений есть нормальное распределение случайных величин.

6. Равномерное распределение на отрезке

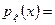
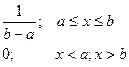
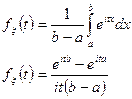
Если рассматривается симметрический отрезок [-l;l]

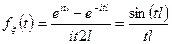
Теорема: Любой характеристической функции соответствует и при том единственная функция распределения (плотность распределения).