Теорема Чебышева.

Пусть 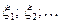попарно независимые случайные величины, имеющие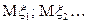

и 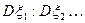. Пусть также дисперсии всех случайных величин ограниченны некоторой константой, т.е. 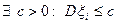, тогда 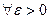выполняется следующее соотношение: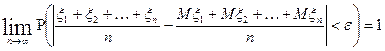

Доказательство:

Воспользуемся вторым неравенством Чебышева.

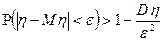
Пусть ; ;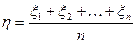

; ;

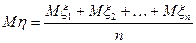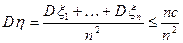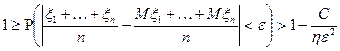
Смысл закона больших чисел заключается в том, что при больших n, с вероятностью близкой к 1, среднее арифметическое суммы независимых случайных величин становится близким к const, равной среднему арифметическому математических ожиданий этих случайных величин.

Следствие теоремы Чебышева: Если при условиях теоремы Чебышева 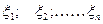имеют равные между собой математические ожидания 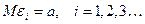, то

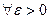
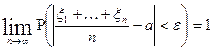
Следствие теоремы Чебышева обосновывает принцип среднего арифметического, используемого во всех экспериментальных дисциплинах, т.е. если производится серия n – измерений без систематической ошибки, то среднее арифметическое результатов наблюдается при больших n сколько угодно мало отличается от измеряемой величины.