Некоторые важнейшие распределения связанные с нормальным.
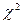 - распределение.
- распределение.

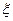 - случайная величина, нормально распределенная с параметрами (0: 1), тогда случайная величина
- случайная величина, нормально распределенная с параметрами (0: 1), тогда случайная величина 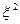 имеет следующую плотность распределения:
имеет следующую плотность распределения:
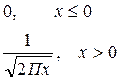
Пусть, 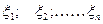 - совокупность n независимых нормально распределенных случайных величин с параметрами (0;1), тогда случайная величина
- совокупность n независимых нормально распределенных случайных величин с параметрами (0;1), тогда случайная величина 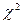 =
= 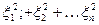 обладает распределением, которое принято называть
обладает распределением, которое принято называть 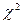 - распределением с n степенями свободы.
- распределением с n степенями свободы.
Свойства 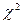 - распределния:
- распределния:
1. Плотность 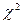 - распределения.
- распределения.

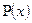 =
= 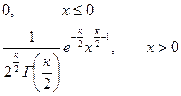
Гамма функция.
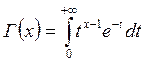
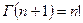
Плотность 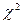 - распределения исключительно зависит от степеней свободы к.
- распределения исключительно зависит от степеней свободы к.
2.
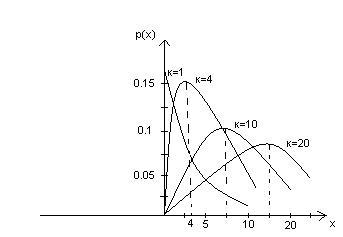
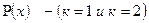 являются монотонно убывающими.
являются монотонно убывающими.
При к = 3 : х = к-2 есть локальный максимум.
3. 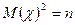
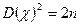
4. С увеличением к – числа степеней свободы 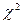 - распределение медленно приближается к нормальному.
- распределение медленно приближается к нормальному.
Распределение Стьюдента ( t – распределение)
Пусть случайные величины 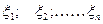 нормально распределены с параметрами
нормально распределены с параметрами  , тогда случайная величина
, тогда случайная величина 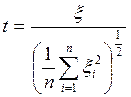 имеет распределение, которое называется t – распределением или распределением Стьюдента с n – степенями свободы.
имеет распределение, которое называется t – распределением или распределением Стьюдента с n – степенями свободы.
1) Р(х) = 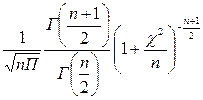 - четная функция
- четная функция
2) По мере увеличения n, распределение Стьюдента быстро приближается к нормальному.
Распределение Фишера-Снедекора ( F – распределение).
Пусть 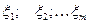 и
и 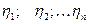 нормально распределены с параметрами (0; 1). Распределение случайной величины вида:
нормально распределены с параметрами (0; 1). Распределение случайной величины вида:

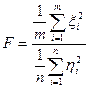 называется распределением со степенями свободы т и п.
называется распределением со степенями свободы т и п.
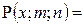

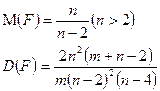
Дата добавления: 2015-07-30; просмотров: 843;
