Основные свойства кривой Гаусса

1. 
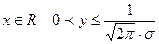
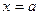2. ось симметрии
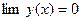3. при
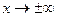
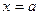4. точка max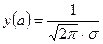
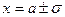5. точки перегиба

σ = 3

σ = 1

σ = 8

При увеличении σ уменьшается амплитуда, и график становится более пологим

2. Основные характеристики нормального распределения

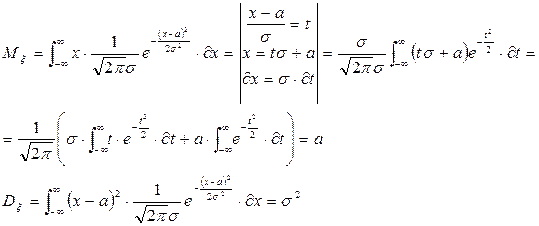
3. Вероятность попадания нормально распределенной случайной величины на заданный отрезок

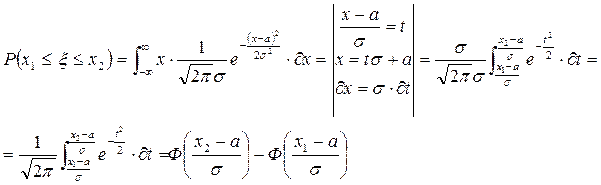
4. Отклонение нормально распределенной случайной величины от её математического ожидания

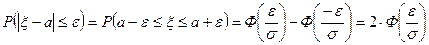
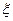
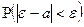
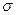
	0.6826
2	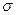0.9544
3	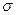0.9973
4	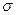0.9994

Правило трех сигм:

Если случайная величина распределена нормально, то считается практически невозможным ее отклонение от М 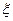больше, чем на 3 .

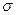Более того, на практике, если некоторая случайная величина отклоняется от своего среднего значения меньше чем на 3 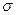, то есть основание предполагать, что эта случайная величина нормально распределенная.