Основні теоретичні відомості. Закон Гука для деформації розтягу (стиску):

Закон Гука для деформації розтягу (стиску):

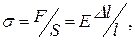
де s – нормальна напруга;

F – деформуюча сила;

S – площа поперечного перерізу;

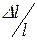– відносна зміна довжини стержня,

E – модуль Юнга.

Коефіцієнт Пуассона:

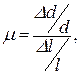
де 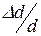– відносна зміна діаметра стержня.

Руйнівна сила:

F_p = s_pS,

де s_p – руйнівна напруга.

У випадку деформації зсуву

s_t = gG,

де 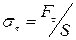– тангенціальна напруга;

G – модуль зсуву;

g – відносний зсув (g = tg j, j – кут зсуву).

Модуль Юнга E, модуль зсуву G і коефіцієнт Пуассона m пов'язані співвідношенням

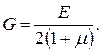
Для закручування стержня (дротини) на деякий кут j необхідно прикласти момент пари сил

M = bj,

де 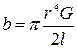– модуль кручення матеріалу;

G – модуль зсуву;

r – радіус стержня;

l – його довжина.

Потенціальна енергія пружно деформованого стержня

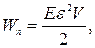
де E – модуль Юнга;

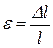– відносна деформація;

V – об'єм стержня.

Питома густина енергії пружно деформованого стержня

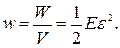
196. Стальний трос, який може витримати вагу нерухомої кабіни ліфта, має діаметр 9 мм. Який діаметр повинен мати трос, щоб кабіна ліфта могла мати прискорення до 8 g?

197. На скільки розтягується залізний стержень, підвішений за один кінець, під дією власної ваги?

198. Вантаж підвішено на трьох тросах. Троси виготовлені з одного матеріалу, а два крайні троси мають однакову довжину. Знайти співвідношення між напруженнями в матеріалі тросів, якщо деформації, якщо є навантаження, дуже малі.

199. Пружний стержень масою m, довжиною l і площею поперечного перерізу s рухається в повздовжньому напрямку з прискоренням а, однаковим для всіх точок стержня. Знайти пружну енергію деформації, що виникає в стержні внаслідок рівноприскореного руху.

200. Коефіцієнт лінійного теплового розширення деякого сплаву дорівнює 1,2·10^­‑5 град.^‑1, а модуль Юнга – 1,5·10¹¹ Н/м². Який тиск потрібно прикласти до торців циліндра із сплаву, щоб його довжина не змінювалась у процесі нагрівання від 20° до 120°C.

201. На невагомому стержні висить вантаж, вага якого дорівнює P. Вантаж відхиляють на 90° і відпускають. Визначити натяг стержня у момент проходження ним положення рівноваги.

202. Вантаж масою 0,3 кг прив'язали до гумового шнура довжиною 15 см, відхилили на 90°С і відпустили. Визначити довжину l гумового шнура в момент проходження вантажем положення рівноваги. Коефіцієнт жорсткості гумового шнура k = 0,5 Н/см.

203. Акробат скаче на сітку з висоти Н₁ = 6 м. На якій граничній висоті над підлогою треба натягнути сітку, щоб акробат не вдарився до підлоги, виконуючи стрибки. Відомо, що сітка прогинається на 0,5 м, якщо акробат скаче на неї з висоти Н₂ = 1 м. Деформацію сітки вважати пружною.

204. З якою швидкістю рухався вагон масою 2·10⁴ кг, якщо внаслідок удару об стінку кожен буфер стиснувся на 10 см? Відомо, що пружина кожного буфера стискається на 1 см під дією сили 10⁴ Н.

205. Тонкий однорідний мідний стержень довжиною l і масою m рівномірно обертається з кутовою швидкістю w у горизонтальній площині навколо вертикальної осі, яка проходить через один з його кінців. Визначити силу натягу в стержні залежно від відстані до осі обертання, а також видовження стержня.

206. Знайти енергію пружної деформації стального стержня масою 3,1 кг, деформованого так, що його відносне видовження становить 1,0·10^‑3.

§ 8. Закон всесвітнього тяжіння.